Viết thành bất phương trình và chỉ ra một nghiệm của nó từ các mệnh đề sau :
a) Tổng của một số nào đó và 5 lớn 7
b) Hiệu của 9 và một số nào đó nhỏ hơn -12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

9 – x < -12
Ta có x = 22 là nghiệm của bất phương trình vì 9 – 22 = -13 < -12

x + 5 > 7
Ta có x = 3 là nghiệm của bất phương trình vì 3 + 5 = 8 > 7

a. $2x + 3 > 12$
Ta có: x = 6 và x = 7 là nghiệm của bất phương trình vì:
$2.6+3=15>12$ và $2.7+3=17>12$
b. $5 – 3x < 10$
Ta có: $x = 1$ và $x = 2$ là nghiệm của bất phương trình vì:
$5–3.1=2<10$ và $5–3.2=–1<10$
a. 2x + 3 > 12
Ta có: x = 6 và x = 7 là nghiệm của bất phương trình vì:
2.6 + 3 = 15 > 12 và 2.7 + 3 = 17 > 12
b. 5 – 3x < 10
Ta có: x = 1 và x = 2 là nghiệm của bất phương trình vì:
5 – 3.1 = 2 < 10 và 5 – 3.2 = -1 < 10

2x + 3 > 12
Ta có: x = 6 và x = 7 là nghiệm của bất phương trình vì:
2.6 + 3 = 15 > 12 và 2.7 + 3 = 17 > 12

5 – 3x < 10
Ta có: x = 1 và x = 2 là nghiệm của bất phương trình vì:
5 – 3.1 = 2 < 10 và 5 – 3.2 = -1 < 10

a) Ta có: 2. (-2) ≤ 3 nên -2 có là nghiệm của bất phương trình
+) 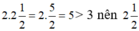 không là nghiệm của bất phương trình ,
không là nghiệm của bất phương trình ,
+) 2π > 3 nên π không là nghiệm của bất phương trình.
+) 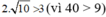 nên √10 không là nghiệm của bất phương trình,
nên √10 không là nghiệm của bất phương trình,
Các số là nghiệm của bất phương trình trên là: -2;
Các số không là nghiệm của bất phương trình trên là: 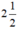 ; π; √10
; π; √10
b)2x ≤ 3 ⇔ x ≤ 3/2
Biểu diễn tập nghiệm trên trục số là:


a) Điều kiện cần và đủ để một số chia hết cho 9 là tổng các chữ số của nó chia hết cho 9.
b) Một hình bình hành có các đường chéo vuông góc là điều kiện cần và đủ để nó là một hình thoi.
c) Để phương trình bậc hai có hai nghiệm phân biệt, điều kiện cần và đủ là biệt thức của nó dương.
a. x + 5 > 7
Ta có x = 3 là nghiệm của bất phương trình vì 3 + 5 = 8 > 7
b. 9 – x < 12
Ta có x = 22 là nghiệm của bất phương trình vì 9 – 22 = -13 < -12