GIÚP MIK CÂU C Ạ, CAMON <3
Bài 2. Cho tam giác ABC có các đường cao BK và CI cắt nhau tại H. Các đường thẳng kẻ từ B và vuông góc với AB, kẻ từ C và vuông góc với AC cắt nhau tại D. a) CMR: Tứ giác BHCD là hình bình hành. b) CMR: AI. AB = AK. AC c) Tam giác AIC đồng dạng với tam giác AKB


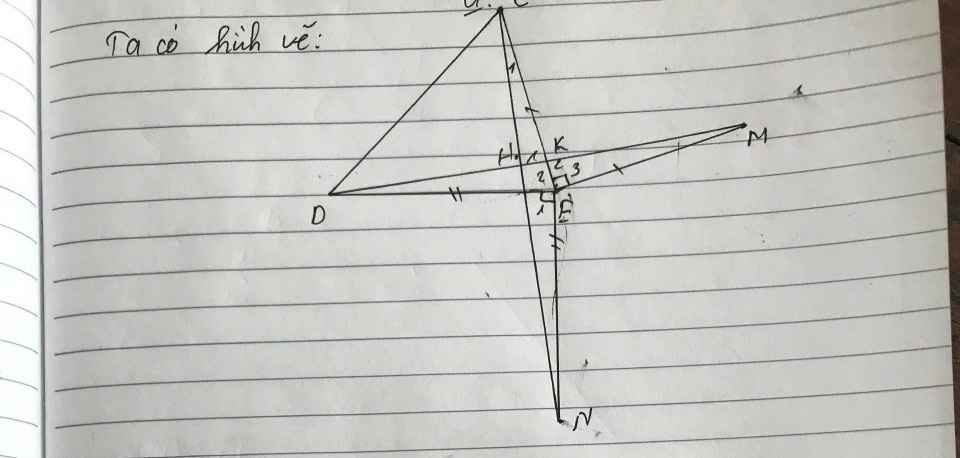









a: Xét tứ giác BHCD có
CH//BD
BH//CD
Do đó: BHCD là hình bình hành
b: Xét ΔAIC vuông tại I và ΔAKB vuông tại K có
\(\widehat{A}\) chung
Do đó: ΔAIC\(\sim\)ΔAKB
Suy ra: \(\dfrac{AI}{AK}=\dfrac{AC}{AB}\)
hay \(AI\cdot AB=AK\cdot AC\)