Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy. Vẽ về một phía của AB các tam giác đều AMD, BME. Trung điểm I của DE di chuyển trên đường nào ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 2 2017
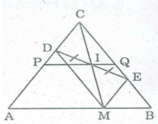
Gọi C là giao điểm của AD và BE.
Tam giác ABC có:
∠ A = 60 0 (vì ΔADM đều)
∠ B = 60 0 ( vì ΔBEM đều)
Nên ∠ C = 180 0 - ∠ A - ∠ B = 60 0
Suy ra: ∆ ABC đều hay AB = AC = BC
Suy ra điểm C cố định.
Lại có: ∠ A = ∠ (EMB ) = 60 0
ME // AC ( vì có cặp góc đồng vị bằng nhau)
Hay ME // CD.
Do ∠ DMA = ∠ BEM = 60 0 ( hai tam giác AMD và BME là tam giác đều )
Suy ra: MD // BC ( vì có cặp góc so le trong bằng nhau ).
hay MD // EC
suy ra tứ giác CDME là hình bình hành.
I là trung điểm của DE nên I là trung điểm của CM
Kẻ CH ⊥ AB,IK ⊥ AB⇒IK // CH
Trong ∆ CHM,ta có:CI = IM và IK // CH
Suy ra IK là đường trung bình của ΔCHM⇒IK = 1/2 CH
Vì C cố định nên CH không đổi ⇒ IK = 1/2 CH không đổi nên I chuyển động trên đường thẳng song song với AB, cách AB một khoảng bằng 1/2 CH
Khi M trùng với A thì I trùng với trung điểm P của AC.
Khi M trùng với B thì I trùng với trung điểm Q của BC.
Vậy khi M chuyển động trên đoạn thẳng AB thì I chuyển động trên đoạn PQ ( P là trung điểm AC, Q là trung điểm BC).
CM
31 tháng 1 2018
Tương tự 2B. Gợi ý: Kéo dài AC và BD cắt nhau tại E. Xét các trường hợp khi M º A Þ C º A, D º E và khi M º B Þ D º B, C º E.
Từ đó chứng minh được I thuộc đường trung bình của DABE.
CM
6 tháng 12 2018
Tương tự bài 4. kéo dài AC và BD cắt nhau tại E. Từ đó chứng minh được I thuộc đường trung bình của DABE.
Gọi giao điểm của AD và BE là C.
∆ ABC có: ˆA=600A^=600 (vì ∆ ADM đều)
ˆB=600B^=600 (vì ∆ BEM đều)
Suy ra: ∆ ABC đều, AC = AB = BC nên điểm C cố định
ˆA=ˆEMB=600A^=EMB^=600
⇒ ME // AC (vì có cặp góc đồng vị bằng nhau)
hay ME // DC
ˆDMA=ˆB=600DMA^=B^=600
⇒ MD // BC (vì có cặp góc đồng vị bằng nhau)
hay MD // EC
Tứ giác CDME là hình bình hành
I là trung điểm của DE nên I là trung điểm của CM
Kẻ CH ⊥ AB, IK ⊥ AB ⇒ IK // CH
Trong ∆ CHM ta có:
CI = IM
IK // CH
nên IK là đường trung bình của ∆ CHM ⇒ IK = 1212CH
C cố định ⇒ CH không đổi ⇒ IK =1212CH không thay đổi nên I chuyển động trên đường thẳng song song AB, cách AB một khoảng bằng 1212CH.
Khi M trùng với A thì I trùng trung điểm P của AC.
Khi M trùng với B thì I trùng với trung điểm Q của BC.
Vậy khi M chuyển động trên đoạn thẳng AB thì I chuyển động trên đoạn PQ (P là trung điểm của AC, Q là trung điểm của BC)
Xem thêm tại: http://sachbaitap.com/cau-129-trang-96-sach-bai-tap-sbt-toan-8-tap-1-c6a8515.html#ixzz4zLYSfxii