Cho tam giác ABC vuông cân tại A, AC = 4cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB, AC
a) Tứ giác ADME là hình gì ? Tính chu vi của tứ giác đó
b) Điểm M ở vị trí nào trên cạnh BC thì đoạn thẳng DE có độ dài nhỏ nhất ?

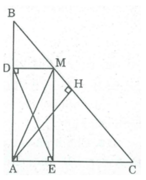
Ta có \(DE=AM\ge AH\). Dấu " = " xảy ra khi \(M\equiv H\)
Vậy DE có độ dài nhỏ nhất là AH khi điểm M là trung điểm của BC.