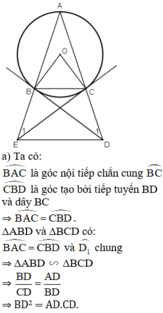
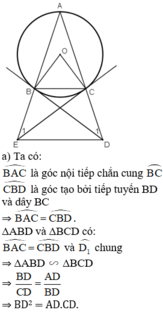
Tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn (O). Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và tia AB ở D và E. Chứng minh :
a) \(BD^2=AD.CD\)
b) Tứ giác BCDE là tứ giác nội tiếp
c) BC song song với DE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b) ΔABC cân tại A
⇒ AB = AC
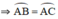
 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
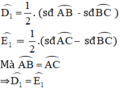
⇒ D và E cùng nhìn BC dưới 1 góc bằng nhau
⇒ BCDE là tứ giác nội tiếp.
c. Tứ giác BCDE nội tiếp

⇒ BC // DE (hai góc đồng vị bằng nhau).

b) ΔABC cân tại A
⇒ AB = AC
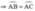
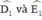 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
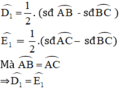
⇒ D và E cùng nhìn BC dưới 1 góc bằng nhau
⇒ BCDE là tứ giác nội tiếp.
c. Tứ giác BCDE nội tiếp

⇒ BC // DE (hai góc đồng vị bằng nhau).

a) Xét ΔADB∆ADB và ΔBDC∆BDC, ta có:
ˆBAD=ˆCBDBAD^=CBD^ (góc nội tiếp cùng chắn cung BCBC)
ˆD1D1^ góc chung
Vậy ΔADB∆ADB đồng dạng ΔBDC∆BDC ⇒ BDCD=ADBD=BD2=AD.CDBDCD=ADBD=BD2=AD.CD (đpcm)
b) Ta có ˆAECAEC^ là góc có đỉnh ở bên ngoài (O)(O)
Quảng cáo
ˆAEC=sđAC−sđBC2=sđAB−sđBC2=ˆADBAEC^=sđAC⏜−sđBC⏜2=sđAB⏜−sđBC⏜2=ADB^
Xét tứ giác BCDEBCDE, ta có: ˆAECAEC^ và ˆADBADB^ là hai góc liên tiếp cùng nhìn đoạn BCBC và ˆAEC=ˆADBAEC^=ADB^ . Vậy tứ giác BCDEBCDE nội tiếp đường tròn
c) Ta có: ˆACB+ˆBCD=1800ACB^+BCD^=1800 (hai góc kề bù).
hay ˆABC+ˆBCD=1800ABC^+BCD^=1800 (ΔABC∆ABC cân tại AA)
⇒ˆABC=1800–ˆBCD(1)⇒ABC^=1800–BCD^(1)
Vì BCDEBCDE là tứ giác nội tiếp nên
ˆBED+ˆBCD=1800⇒ˆBED=1800–ˆBCD(2)BED^+BCD^=1800⇒BED^=1800–BCD^(2)
So sánh (1) và (2), ta có: ˆABC=ˆBEDABC^=BED^
Ta cũng có: ˆABCABC^ và ˆBEDBED^ là hai góc đồng vị. Suy ra: BC//DEBC//DE (đpcm)
a) Xét ΔADB∆ADB và ΔBDC∆BDC, ta có:
ˆBAD=ˆCBDBAD^=CBD^ (góc nội tiếp cùng chắn cung BCBC)
ˆD1D1^ góc chung
Vậy ΔADB∆ADB đồng dạng ΔBDC∆BDC ⇒ BDCD=ADBD=BD2=AD.CDBDCD=ADBD=BD2=AD.CD (đpcm)
b) Ta có ˆAECAEC^ là góc có đỉnh ở bên ngoài (O)(O)
Quảng cáo
ˆAEC=sđAC−sđBC2=sđAB−sđBC2=ˆADBAEC^=sđAC⏜−sđBC⏜2=sđAB⏜−sđBC⏜2=ADB^
Xét tứ giác BCDEBCDE, ta có: ˆAECAEC^ và ˆADBADB^ là hai góc liên tiếp cùng nhìn đoạn BCBC và ˆAEC=ˆADBAEC^=ADB^ . Vậy tứ giác BCDEBCDE nội tiếp đường tròn
c) Ta có: ˆACB+ˆBCD=1800ACB^+BCD^=1800 (hai góc kề bù).
hay ˆABC+ˆBCD=1800ABC^+BCD^=1800 (ΔABC∆ABC cân tại AA)
⇒ˆABC=1800–ˆBCD(1)⇒ABC^=1800–BCD^(1)
Vì BCDEBCDE là tứ giác nội tiếp nên
ˆBED+ˆBCD=1800⇒ˆBED=1800–ˆBCD(2)BED^+BCD^=1800⇒BED^=1800–BCD^(2)
So sánh (1) và (2), ta có: ˆABC=ˆBEDABC^=BED^
Ta cũng có: ˆABCABC^ và ˆBEDBED^ là hai góc đồng vị. Suy ra: BC//DEBC//DE (đpcm)

câu c. chứng minh hai góc trong cùng phía bù nhau góc BCD và CDE
Làm câu c) thôi ạ ._.
c) Tứ giác BCDE nội tiếp :
\(\Rightarrow\widehat{BED}+\widehat{BCD}=180^o\)
Mà \(\widehat{BCD}+\widehat{ACD}=180^o\)( hai góc kề bù )
\(\Rightarrow\widehat{BED}=\widehat{ACB}\)
Mà \(\widehat{ACB}=\widehat{ABC}\)( \(\Delta ABC\)cân tại A )
\(\Rightarrow\widehat{BED}=\widehat{ABC}\)
=> BC // DE ( hai góc đồng vị bằng nhau )