Từ một điểm P ở ngoài đường tròn (O), kẻ hai cát tuyến PAB và PCD tới đường tròn. Gọi Q là một điểm nằm trên cung nhỏ BD (không chứa A và C) sao cho số đó \(\widehat{BQ}=42^0\) và sđ \(\widehat{QD}=38^0\). Tính tổng \(\widehat{BPD}+\widehat{AQC}\) ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
22 tháng 8 2021
a) AD và AF cách đều tâm O nên chúng bằng nhau.
b) Kẻ OI MN, OK PQ.
Trong đường tròn nhỏ, ta có: MN > PQ OI < OK.
(Dây lớn hơn thì gần tâm hơn)
Trong đường tròn lớn, OI < OK AE > AH.
(Dây gần tâm hơn thì lớn hơn)
c) A, B, O, C cách đều trung điểm AO.
d)
18 tháng 1 2021
Từ gt => \(\Delta OAB\) vuông tại B và \(\Delta OAC\) vuông tại C
\(\Rightarrow\widehat{OAB}+\widehat{AOB}=90^o,\widehat{OAC}+\widehat{AOC}=90^o\)
\(\Rightarrow\left(\widehat{OAB}+\widehat{OAC}\right)+\left(\widehat{AOB}+\widehat{AOC}\right)=180^O\)
Hay \(\widehat{BAC}+\widehat{BOC}=180^O\Rightarrow\widehat{BOC}=180^o-\alpha\)
\(\Rightarrow\) số đo \(\widebat{BmC}=180^o-\alpha\) và số đo \(\widebat{BnC=180^o+\alpha}\)
4 tháng 7 2023
a: góc CAF=1/2(sđ cung CF-sđ cung BE)
=>1/2(sđ cung CF-30)=45
=>sđ cung CF-30=90
=>sđ cung CF=120 độ
b: góc BIE=1/2(sđ cug BE+sđ cung CF)=75 độ
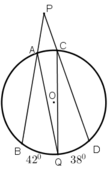
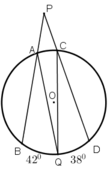
Hướng dẫn làm bài:
Ta có ˆBPDBPD^ là góc ở ngoài đường tròn (O) nên:
ˆBPD=sđcungBQD−sđcungAC2BPD^=sđcungBQD−sđcungAC2
Ta có ˆAQCAQC^ là góc nội tiếp trong đường tròn (O) nên:
ˆAQC=12sđcungACAQC^=12sđcungAC
Do đó:
ˆBPD+ˆAQC=sđcungBQF−sđcungAC2+sđcungAC2=sđcungBQD2=420+3802=400BPD^+AQC^=sđcungBQF−sđcungAC2+sđcungAC2=sđcungBQD2=420+3802=400
Vậy ˆBPD+ˆAQC=400