Tam giác ABC vuông góc tại C có AC = 15cm. Đường cao CH chia AB thành hai đoạn AH và HB. Biết HB = 16cm. Tính diện tích tam giác ABC ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HH
16 tháng 10 2020
Đặt AH = x ( x > 0 ) , ta có :
\(AC^2=AH.AB\)
\(\Leftrightarrow15^2=x\left(x+16\right)\)
\(\Leftrightarrow x^2+16x-225=0\)
Giải phương trình , ta được : \(x_1=9\)
\(x_2=-25\)( loại )
Vậy AH = 9 , suy ra :
\(CH=\sqrt{AC^2-AH^2}=\sqrt{15^2-9^2}=12\)
=> Diện tích tam giác ABC là :
\(S_{ABC}=\frac{1}{2}AB.CH=\frac{1}{2}\left(9+16\right).12=150\left(cm^{^2}\right)\)
16 tháng 3 2023
3:
\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
HB=12^2/20=7,2cm
=>HC=20-7,2=12,8cm
\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{48\sqrt{2}}{7}\)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{48}{35}\left(cm\right)\)
CM
9 tháng 7 2018
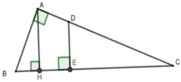
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.
Xét ΔAHC và ΔABC có C chung và A H C ^ = B A C ^ = 90 ∘ nên ΔAHC ~ ΔBAC (g-g)
Ta có S D E C = 1 2 S A B C (1), S A H C : S A B C = H C B C = 9 9 + 3 , 5 = 18 25 2
Từ (1) và (2) suy ra S D E C : S A H C = 1 2 : 18 25 = 25 36 = ( 5 6 ) 2 ( 3 )
Vì DE // AH (cùng vuông với BC) duy ra ΔDEC ~ ΔAHC nên
S D E C : S A H C = ( E C H C ) 2 ( 4 )
Từ (3) và (4) suy ra E C H C = 5 6 tức là E C 9 = 5 6 => EC = 7,5cm.
Đáp án: D
CM
30 tháng 10 2018
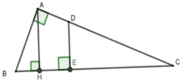
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.
Xét ΔAHC và ΔABC có C chung và A H C ^ = B A C ^ = 90 ∘ nên ΔAHC ~ ΔBAC (g-g)
Ta có S D E C = 1 2 S A B C (1), S A H C : S A B C = 18 25 (2).
Từ (1) và (2) suy ra
S D E C : S A H C = 1 2 : 18 25 = 25 36 = ( 5 6 ) 2 3
Vì DE // AH (cùng vuông với BC) duy ra ΔDEC ~ ΔAHC nên
S D E C : S A H C = ( E C H C ) 2 (4)
Từ (3) và (4) suy ra E C H C = 5 6 tức là E C 18 = 5 6 => EC = 15cm.
Đáp án: A
NH
1
14 tháng 9 2018
Đặt BC=x \(\Rightarrow\)BH=x-16
\(\Rightarrow\)AB2=x(x-16) \(\Leftrightarrow\)152=x(x-16) \(\Leftrightarrow\)x=25
\(\Rightarrow\)BC=25(cm),BH=25-16=9(cm)
AC=\(\sqrt{BC^2-AB^2}\)=20(cm)
AH=\(\sqrt{BH.HC}\)=12(cm
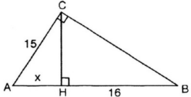
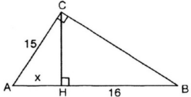
Đặt AH = x (x > 0)
Áp dụng hệ thức lượng trong tam giác vuông ABC, ta có: AC2 = AB.AH
hay 152 = (x + 16)x ⇔ x2 + 16x -225 = 0
Giải phương trình, ta được x1 = 9 (thỏa mãn); x2 = -25 (loại)
Vậy AH = 9 (cm)
Ta có: HC2 = AH. HB = 9. 16 = 144
⇒ HC = 12 (cm)
Vậy diện tích tam gaics ABC là:
S=12AB.CH=12.25.12=150(cm2)