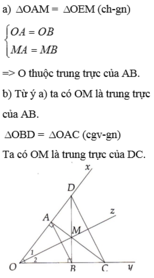
Cho góc xOy có Oz là tia phân giác , M là điểm bất kỳ thuộc tia Oz. Qua M kẻ đường thẳng a vuông góc với Ox tại A cắt Oy tại C và vẽ đường thẳng b vuông góc với Oy tại B cắt tia Ox tại D
a) chứng minh tam giác AOM bằng tam giác BOM từ đó suy ra OM là đường trung trực của đoạn thẳng AB
b) tam giác DMC là tam giác gì ? Vì sao ?
c) chứng minh DM + AM < DC

a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOAM=ΔOBM
Suy ra: OA=OB và MA=MB
=>OM là đường trung trực của AB
b: Xét ΔMAD vuông tại A và ΔMBC vuông tại B có
MA=MB
\(\widehat{AMD}=\widehat{BMC}\)
Do đó: ΔMAD=ΔMBC
Suy ra: MD=MC
hay ΔMDC cân tại M
c: DM+AM<DM
mà DM=DC
nên DM+AM<DC