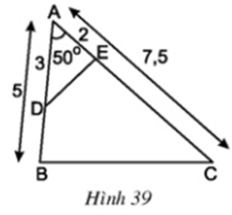
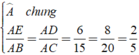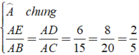Cho tam giác ABC trong đó AB = 15 cm, AC = 80 cm. Trên hai cạnh AB và AC lần lượt lấy hai điểm D và E sao cho AD = 8cm, AE = 6cm. Hai tam giác ABC và ADE có đồng dạng với nhau không ? Vì sao ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LH
Lưu Hạ Vy
22 tháng 4 2017
Đúng(0)
Những câu hỏi liên quan
12 tháng 3 2023
a: Xét ΔABC và ΔAED có
AB/AE=AC/AD
góc A chung
=>ΔABC đồng dạng vơi ΔAED
b: EF//AB
=>EF/AB=CE/CA
=>EF/18=5/8
=>EF=90/8=11,25(cm)
BF/FC=AE/EC=3/5
12 tháng 3 2023
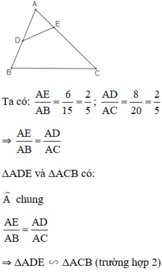
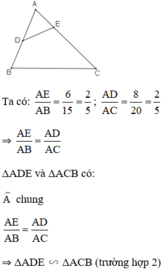
b: Xet ΔAED và ΔABC có
AE/AB=AD/AC
góc A chung
=>ΔAED đồng dạng với ΔABC
6 tháng 3 2022
Sửa đề: Tam giác ABC vuông tại A. Câu c. C/m IB.AD=IC.AE
a.
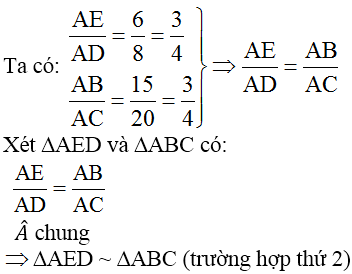
Ta có:
\(\dfrac{AE}{AB}=\dfrac{6}{15}=\dfrac{2}{5};\dfrac{AD}{AC}=\dfrac{8}{20}=\dfrac{2}{5}\)
\(\Rightarrow\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
Xét tam giác ABC và tam giác AED,có:
\(\dfrac{AE}{AB}=\dfrac{AD}{AC}\) ( cmt )
\(\widehat{A}:chung\)
Vậy tam giác ABC dồng dạng tam giác AED ( c.g.c )
b.
Áp dụng định lý pitago vào tam giác vuông ABC, có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{15^2+20^2}=\sqrt{625}=25cm\)
Ta có: tam giác ABC dồng dạng tam giác AED ( c.g.c )
\(\Rightarrow\dfrac{AD}{AC}=\dfrac{DE}{BC}\)
\(\Leftrightarrow\dfrac{2}{5}=\dfrac{DE}{25}\)
\(\Leftrightarrow5DE=50\)
\(\Leftrightarrow DE=10cm\)
c.Áp dụng t/c đường phân giác góc A, ta có:
\(\dfrac{AB}{AC}=\dfrac{IB}{IC}\)
Mà \(\dfrac{AB}{AC}=\dfrac{AE}{AD}\) ( 2 tam giác đồng dạng )
\(\Rightarrow\dfrac{AE}{AD}=\dfrac{IB}{IC}\)
\(\Leftrightarrow IB.AD=IC.AE\)
