Tìm trong các hình 63, 64 các tam giác bằng nhau (các cạnh bằng nhau được đánh dấu bởi những kí hiệu giống nhau). Kể tên các đỉnh tương ứng của các tam giác bằng nhau đó ? Viết kí hiệu về sự bằng nhau của các tam giác đó ?

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Xem hình 63)
Ta có:
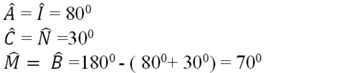
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
QUẢNG CÁO- Xem hình 64)
ΔPQR có:
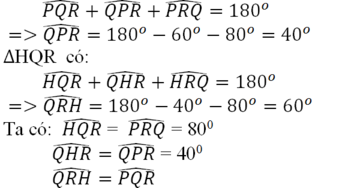
Và QH = RP, HR = PQ, QR cạnh chung
Nên ΔHQR = ΔPRQ

Hình 63
Ta có:
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
Hình 64 :
ΔPQR có:
Và QH = RP, HR = PQ, QR ( cạnh chung )
Nên ΔHQR = ΔPRQ

Hai tam giác bằng nhau vì có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau
kí hiệu: ΔABC = ΔMNP

tam giác ABC và tam giác HIK . vì AB = KI , góc B = góc K .
suy ra : AC=IH ; BC = KH
Xem hình a) ta có:
\(\widehat{A}=\widehat{I}=80^0\) ; \(\widehat{C}=\widehat{N}=30^0\)
\(\widehat{B}=\widehat{M}=180^0-\left(80^0+30^0\right)=70^0\)
Và AB=MI, AC=IN, BC=MN.
nên ∆ABC=∆IMN
Xem hình b) ta có:
\(\widehat{Q}_2=\widehat{R}_2=80^0\)=800 (ở vị trí so le trong)
Nên QH// RP
Nên \(\widehat{R}_1=\widehat{Q}_1\)= 600(so le trong)
\(\widehat{P}=\widehat{H}\)= 400
và QH= RP, HR= PQ, QR chung.
nên ∆HQR=∆PRQ.
Xem hình a) ta có:
ˆAA^=ˆII^=800,ˆCC^=ˆNN^=300
ˆBB^=ˆMM^=1800-(800+300)=700
Và AB=MI, AC=IN, BC=MN.
nên ∆ABC=∆IMN
Xem hình b) ta có:
ˆQ2Q2^=ˆR2R2^=800 (ở vị trí so le trong)
Nên QH// RP
Nên ˆR1R1^ = ˆQ1Q1^= 600(so le trong)
ˆPP^=ˆHH^= 400
và QH= RP, HR= PQ, QR chung.
nên ∆HQR=∆PRQ.