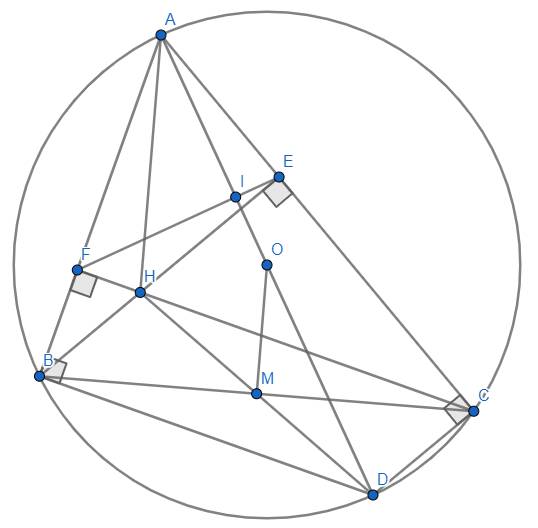
Cho tam giác ABC là tam giác nhọn và nội tiếp đường tròn (O), AB bé hơn AC. Các đường cao BI, CK của tam giác ABC cắt nhau tại H. Kẻ đường kính AD của đường tròn (O).
a) Tứ giác BHCD là hình gì?
b) Các đoạn thẳng BC và HD cắt nhau tại M. Chứng minh AH = 2.OM.
c) Chứng minh tam giác AHD và tam giác ABC có cùng trọng tâm.

a, C thuộc đường tròn đk AD (gt) => ^ACD = 90 => AC _|_ CD mà có BH _|_ AC => CD // BH
B thuộc đường tròn đk AD (gt) => ^ABD = 90 => AB _|_ BD mà có CH _|_ AB => BD // CH
=> BHCD là hình bình hành
b, có BHCD là hình bình hành => M là trung điểm của HD
Có O là trung điểm của AD do AD là đường kính
=> MO là đường trung bình của tam giác AHD
=> MO = 1/2AH
=> AH = 2MO
c, Gọi AM cắt HO tại N
=> N là trọng tâm của tam giác AHD
=> AN = 2/3AM
mà có AM là đường trung tuyến của tam giác ABC
=> H là trọng tâm của tam giác ABC
ờm câu c cũng không chắc lắm