Trong kì thi tuyển sinh vào lớp 10, tại 1 phòng thi có 24 thí sinh. Các thí sinh đều làm bài trên tờ giấy thi của mình. Sau khu thu bài, cán bộ giám thị đếm được 33 tờ giấy thi và bài làm của thí sinh là 1 hoặc 2 tờ. Hỏi có bao nhiêu thí sinh làm 1 tờ, bao nhiêu thí sinh làm 2 tờ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số thí sinh làm bài chỉ gồm 1 tờ giấy thi là x ( đk : x \(\in\) N* ; X < 24 )
Số thí sinh làm bài gồm 2 tờ giấy thi là y ( đk y\(\in\) N* ; y < 24 )
Do một phòng thi có 24 thí sinh dự thi nên ta có phương trình
x + y = 24 ( 1 )
Sau khi thu bài cán bộ coi thi đếm được 33 tờ giấy thi nên ta có phương trình : x + 2y = 33 ( 2 )
Từ ( 1 ) và ( 2 ) ta có hệ phương trình
\(\hept{\begin{cases}x+y=24\\x+2y=33\end{cases}\Leftrightarrow\hept{\begin{cases}x=15\\y=9\end{cases}\left(TM\right)}}\)
Vậy có 15 thí sinh làm bài gồm 1 tờ giấy thi , có 9 thí sinh làm bài gồm 2 tờ giấy thi

Nếu bài kiểm tra của 24 thí sinh đó đều làm 2 tờ giấy thi thì số tờ giấy là:
24.2 = 48 (tờ)
Mà chỉ có 33 tờ giấy nên số tờ giấy nhiều hơn so với đề bài nếu 24 thí sinh đó đều làm 2 tờ giấy chính bằng số thí sinh làm 1 tờ giấy thi và là:
48 - 33 = 15 (thí sinh)
Số thi sinh làm 2 tờ giấy thi là:
24 - 15 = 9 (thí sinh)

Tổng số HS làm 1 - 2 tờ:
24 - 3 = 21 (học sinh)
Tổng số giấy làm bài của 21 học sinh làm từ 1-2 tờ:
43 - 3 x 3 = 34 (tờ)
Gọi a,b lần lượt là số học sinh làm 1 tờ giấy, 2 tờ giấy trong kì thi tuyển sinh vào 10 đó. (0<a,b<21. a và b là số tự nhiên)
Vì tổng số hs làm 1-2 tờ là 21 hs nên ta có pt (1): a+b=21
Vì tổng số giấy 21 hs này làm là 34 tờ nên ta có pt (2): a+ 2b=34
Từ pt (1) và (2), ta lập hệ pt:
\(\left\{{}\begin{matrix}a+b=21\\a+2b=34\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=8\left(TM\right)\\b=13\left(TM\right)\end{matrix}\right.\)
Vậy có 8 thí sinh là 1 tờ giấy, 13 thí sinh làm 2 tờ giấy

Chọn C.
Phương pháp:

Gọi A : “bạn Nam có đúng 2 lần ngồi vào cùng 1 vị trí”
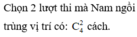
Trong 2 lượt đó, lượt đầu: Nam có 24 cách chọn vị trí, có 23! cách xếp vị trí cho 23 thí sinh còn lại; lượt sau: Nam có 1 cách chọn vị trí, có 23! cách xếp vị trí cho 23 thí sinh còn lại.
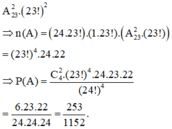


Gọi số thí sinh làm bài chỉ có 1 tờ giấy thi là x ( thí sinh); x∈N*, x<24
Gọi số thí sinh làm bài gồm 2 tờ giấy thi là y ( thí sinh); x∈N*, x<24
1 phòng thi có 24 thí sinh nên ta có: x+y=24 (1)
Sau khi thi bài cán bộ coi thi đếm được tổng có 33 tờ giấy thi nên ta có phương trình sau: x+2y=33
Từ (1) và (2) ta có hệ sau: x + y = 24
x + 2y = 33
=> x=15; y=9
Vậy tất cả có 15 thí sinh làm bài 1 tờ giấy thi và cps 9 thí sinh làm bài gồm 2 tờ giấy thi.
Số hs làm hai tờ là: 33-24= 9 (hs) (Vì bài làm chỉ có thể có 1 hoặc 2 tờ) Số hs lam một tờ là: 24-9= 15 (hs)