Một vật có khối lượng m = 20g đặt ở mép một chiếc bàn quay. Hỏi phải quay bàn với tần số vòng lớn nhất là bao nhiêu để vật không bị văng ra khỏi bàn? Cho biết mặt bàn hình tròn, bán kính 1m. Lực ma sát nghỉ cực đại bằng 0,08N.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
30 tháng 9 2018
Ta có:
+ f = 1 T = ω 2 π → ω = 2 π f
+ Lực hướng tâm tác dụng vào vật: F h t = m ω 2 r = m 2 π f 2 r
+ Để vật không văng ra khỏi mặt bàn, ta phải có:
F h t = F m s n max ↔ m 2 π f 2 r = F m s n max → f 2 = F m s n max m 4 π 2 r = 0 , 08 20.10 − 3 .4 π 2 .1 = 0 , 101 → f ≈ 0 , 32 s − 1
Vậy muốn vật không bị văng ra khỏi mặt bàn thì tần số quay của bàn lớn nhất là: f = 0 , 32 s − 1
Đáp án: A
HY
20 tháng 1 2016
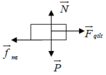
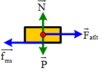
Chọn hệ quy chiếu gắn với mặt đất.
Áp dụng định luật II Niutơn:(do vật quay đểu nên tổng hợp lực là lực hướng tâm)
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}} = \overrightarrow{F_{ht}}\)
Chiếu hướng tâm phương trình trên ta được:
\(0+0+F_{ms} = F_{ht}\)
=> \(F_{ms} = ma_{ht}\)
Để vật không bị văng ra khi bàn quay thì
\(F_{ms} \leq F_{msn MAX}\)
=> \(ma_{ht} \leq 0.08N\)
=>\(m\omega ^2 R\leq 0.08N\)
=>\(\omega \leq \sqrt{\frac{0.08}{0.02.1}} = 2 rad/s.\)
Vậy để vật không bị văng ra khỏi mặt bàn thì tần số góc của bàn phải nhỏ hơn 2 rad/s.
VT
27 tháng 5 2017
Ta có:
+ f = 1 T = ω 2 π → ω = 2 π f
+ Lực hướng tâm tác dụng vào vật: F h t = m ω 2 r = m 2 π f 2 r
+ Để vật không văng ra khỏi mặt bàn, ta phải có:
F = F m s n max ↔ m 2 π f 2 r = F m s n max → f 2 = F m s n max m 4 π 2 r = 0 , 08 20.10 − 3 .4 π 2 .1 = 0 , 101 → f ≈ 0 , 32 s − 1
Vậy muốn vật không bị văng ra khỏi mặt bàn thì tần số quay của bàn lớn nhất là: f = 0 , 32 s − 1
=> Chu kì nhỏ nhất là: T min = 1 f max = 1 32 ≈ 3,12 ( s )
Đáp án: A
VT
10 tháng 12 2019
Để vật không bị văng ra ngoài khỏi bàn thì: Fht ≤ Fmsn (max)
(Khi Fmsn (max) ≤ Fht thì vật bị văng)
Lực hướng tâm tác dụng vào vật:
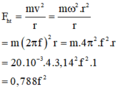
(f là tần số quay của bàn)
Để vật không bị văng ra khỏi mặt bàn ta có:
Fht ≤ Fmsn ⇔ 8.10-2. 9,8596. f2 ≤ 8.10-2
VT
15 tháng 8 2019
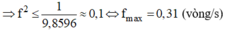
Để vật không bị văng ra khỏi bàn thì lực hướng tâm phải có giá trị bằng lực ma sát nghỉ:
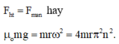
Tần số vòng lớn nhất ứng với lực ma sát nghỉ cực đại:
VT
26 tháng 4 2019
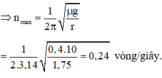
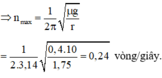
Để vật không bị trượt ra khỏi bàn: F q t l t ≤ F m s
⇒ m ω 2 . r ≤ μ . N = μ . m . g
⇒ ω ≤ μ . g r = 2.10 0 , 8 = 5 r a d / s
VT
21 tháng 5 2019
Chọn đáp án A
Lực ma sát đóng vai trò là lực hướng tâm. Vật không bị văng ra xa tâm bàn khi
VT
26 tháng 1 2017
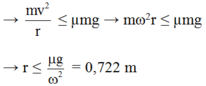
Chọn A.
Lực ma sát đóng vai trò là lực hướng tâm. Vật không bị văng ra xa tâm bàn khi F h t ≤ F m s
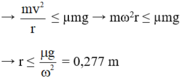
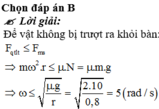
Để vật không bị văng ra khỏi bàn, ta có:
Fmsn(max) = Fht = = m\(\omega\)2r
Fmsn(max) = m.R (2\(\pi\) nmax)2 = mR4\(\pi\)2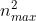
=> nmax =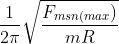
=> nmax =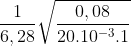
= 
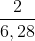
=> nmax = 0,318 vòng/s