Question

[Hồ Hoàng Thành]

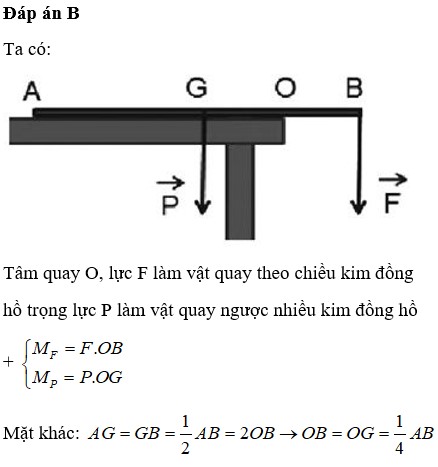
Có một thanh kim loại đồng chất, tiết diện đều, khối lượng m, chiều dài l. Ban đầu, đầu của thanh kim loại đang nằm tại ranh giới của hai nửa mặt bàn làm từ hai chất liệu khác nhau, độ nhám khác nhau. Tính công cần thực hiện để kéo thanh kim loại đi trên mặt bàn và nằm hoàn toàn ở mặt bàn thứ hai. Trọng lượng của thanh kim loại tỉ lệ với lực ma sát, hệ số ma sát của hai nửa mặt bàn là k₁ và k₂.

Answer 1

[Hoàng Nguyên Vũ]

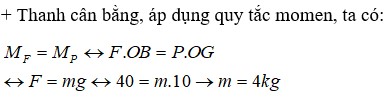
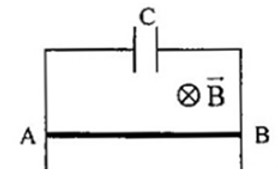
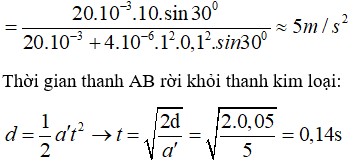
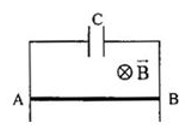
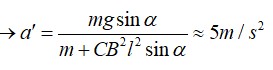
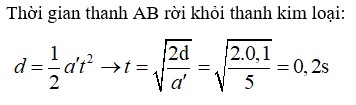
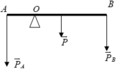
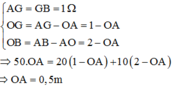
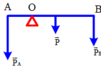
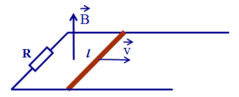
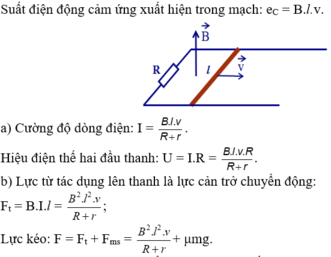
Để kéo thanh kim loại di chuyển thì lực kéo tối thiểu phải bằng lực ma sát. Do hai mặt bàn có lực ma sát khác nhau nên khi kéo thanh kim loại từ mặt bàn thứ nhất sang mặt bàn thứ hai thì độ lớn của lực kéo sẽ thay đổi theo sự thay đổi của ma sát.

Gọi lực kéo là F, trọng lượng của thanh kim loại là P, lực ma sát là F_ms

Muốn kéo thanh kim loại đi đều sang nửa mặt bàn thứ hai thì:

F = F_ms = k.P (k là hệ số ma sát)

Khi thanh kim loại nằm hoàn toàn ở bên mặt bàn thứ nhất thì:

F₁ = F_ms2 = k₁.P = 10m.k₁

Khi thanh kim loại đã được kéo hoàn toàn sang mặt bàn thứ hai thì:

F₂ = F_ms1 = k₂.P = 10m.k₂

Trong quá trình thanh kim loại được kéo sang mặt bàn thứ hai thì thanh di chuyển một đoạn:

s = l (m)

Ta xét hai trường hợp:

* k₁ < k₂ (mặt bàn thứ nhất có lực ma sát nhỏ hơn mặt bàn thứ hai)

Công để kéo thanh kim loại được biểu diễn ở đồ thị dưới đây.

Công A được tính bằng diện tích hình thang ABCD

\(A=\dfrac{\left(OA+OB\right)OC}{2}=\dfrac{\left(10m.k_1+10m.k_2\right).l}{2}\\ =\dfrac{10m\left(k_1+k_2\right).l}{2}=5m\left(k_1+k_2\right).l\)

* k₁ > k₂ (mặt bàn thứ nhất có lực ma sát lớn hơn mặt bàn thứ hai)

Công để kéo thanh kim loại được biểu diễn ở đồ thị dưới đây.

Công A vẫn được tính ra như trên bằng diện tích hình thang ABCD.

\(A=\dfrac{\left(OA+OB\right)OC}{2}=\dfrac{(10m.k_1+10m.k_2)l}{2}=5\left(k_1+k_2\right).l\)

Kết luận: công ở hai trường hợp như nhau và bằng A = 5(k₁ + k₂).l