Cho hai mặt phẳng
\(\left(P_1\right):2x+y+z+1=0\)
\(\left(P_2\right):4x-2y-4z+7=0\)
Lập phương trình mặt phẳng sao cho khoảng cách từ mỗi điểm của nó đến \(\left(P_1\right)\&\left(P_2\right)\) là bằng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyen Thuy Hoa
22 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
CM
1 tháng 1 2019
Ta có: M(x, y, z) ∈ (P) ⇔ d(M, ( P 1 )) = d(M, ( P 2 ))
⇔ 2|2x + y + 2z + 1| = |4x − 2y − 4z + 7|
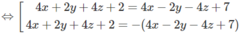
Từ đó suy ra phương trình mặt phẳng phải tìm là: 4y + 8z – 5 = 0 hoặc 8x + 9 = 0
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2019
\(\left\{{}\begin{matrix}\overrightarrow{n_{\left(P1\right)}}=\left(1;-1;1\right)\\\overrightarrow{n_{\left(P2\right)}}=\left(3;2;-12\right)\end{matrix}\right.\) \(\Rightarrow\)\(\left[\overrightarrow{n_{\left(P1\right)}};\overrightarrow{n_{\left(P2\right)}}\right]=\left(10;15;5\right)=5\left(2;3;1\right)\)
Chọn \(\overrightarrow{n_{\left(p\right)}}=\left(2;3;1\right)\) là 1 vtpt của (P)
Phương trình (P): \(2x+3y+z=0\)
Câu 2:
\(\left\{{}\begin{matrix}\overrightarrow{u_d}=\left(2;1;1\right)\\\overrightarrow{u_{d'}}=\left(1;-2;1\right)\end{matrix}\right.\) \(\Rightarrow\left[\overrightarrow{u_d};\overrightarrow{u_{d'}}\right]=\left(3;-1;-5\right)\)
\(\Rightarrow\) Chọn \(\overrightarrow{n_{\alpha}}=\left(3;-1;-5\right)\) là một vtpt của \(\left(\alpha\right)\)
Phương trình \(\left(\alpha\right)\):
\(3\left(x-0\right)-1\left(y-1\right)-5\left(z-2\right)=0\)
\(\Leftrightarrow3x-y-5z+11=0\)
6 tháng 4 2016
\(d\left(A,\left(\alpha\right)\right)=\frac{4}{3}\)
\(\left(\beta\right)\)//\(\left(\alpha\right)\) nên phương trình \(\left(\beta\right)\) có dạng : \(x+2y-2z+d=0,d\ne-1\)
\(d\left(A,\left(\alpha\right)\right)=d\left(A,\left(\beta\right)\right)\)\(\Leftrightarrow\frac{\left|5+d\right|}{3}=\frac{4}{3}\Leftrightarrow\begin{cases}d=-1\\d-9\end{cases}\)\(\Leftrightarrow d=-9\left(d=-1loai\right)\)\(\Rightarrow\left(\beta\right):x+2y-2z-9=0\)
23 tháng 5 2017
Gọi Q là mặt phẳng đi qua A và song song với (P) thì phương trình của (Q) là \(\left(x+2\right)+2\left(y+1\right)-\left(z-1\right)=0\) hay \(x+2y-z+5=0\). Gọi H là hình chiếu vuông góc của B lên (Q). Giả sử \(\Delta\) là đường thẳng qua A và song song với
