Bài 4. Cho ABCD là hình bình hành. Hai điểm M, N lần lượt chuyển động trên các đoạn thẳng AB, CD (M, N khác đỉnh của hình bình hành) thỏa mãn AM = CN. Chứng minh đường thẳng MN luôn đi qua một điểm cố định
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 10 2021
a: Xét tứ giác BMDN có
BM//DN
BM=DN
Do đó: BMDN là hình bình hành
UI
27 tháng 2 2020
De dang chung minh duoc \(\Delta MAX=\Delta MDP,\Delta NBY=\Delta NCP\)
suy ra M la trung diem XP, N la trung diem PY
xet tam giac XPY co YM,XN la duong trung tuyen => T la trong tam tam giac XPY
=> PT di qua trung diem XY (1)
Mat khac MN // XY ( duong trung binh) (2)
va M , N la trung diem AD,BC co dinh (3)
tu (1),(2),(3) suy ra PT di qua trung diem MN co dinh
Chuc ban hoc tot
27 tháng 2 2020
Upin : t nghĩ phần cuối của m từ ( 1 ), ( 2 ) và ( 3 ) => ... như thế không thuyết phục lắm
t nghĩ là m nên nói bổ đề hình thang
còn không thì gọi giao điểm PT với MN và XY là K và H
xong dùng Ta-lét để chứng minh MK = KN
6 tháng 10 2018
Gọi G là trung điểm của CD. Cho MN cắt AG tại I. Ta sẽ chứng minh điểm I cố định.
Thật vậy: Kéo dài tia BG cắt tia AD tại P. Qua 2 điểm B và P kẻ các đường thẳng song song với MN, chúng cắt đường thẳng AG lần lượt ở 2 điểm E và F.
Dễ thấy: \(\Delta\)BGC = \(\Delta\)PGD (g.c.g) => GB = GP (2 cạnh tương ứng)
=> \(\Delta\)BEG = \(\Delta\)PFG (g.c.g) => GE = GF (2 cạnh tương ứng) => EF = 2.GE
Xét \(\Delta\)PAF có: N thuộc AP; I thuộc AF; IN // PF => \(\frac{AP}{AN}=\frac{AF}{AI}=\frac{AE+EF}{AI}=\frac{AE+2.GE}{AI}\)(ĐL Thales)
Do \(\Delta\)BGC = \(\Delta\)PGD (cmt) nên BC = PD. Mà BC = AD => PD = AD = 1/2 .AP
\(\Rightarrow\frac{2.AD}{AN}=\frac{AE+2.GE}{AI}\). Tương tự: \(\frac{AB}{AM}=\frac{AE}{AI}\)
Do đó: \(\frac{AB}{AM}+\frac{2.AD}{AN}=\frac{2\left(AE+GE\right)}{AI}=\frac{2.AG}{AI}\). Suy ra \(\frac{2.AG}{AI}=4\)(Theo gt)
\(\Rightarrow\frac{AG}{AI}=2\)=> I là trung điểm của AG
Ta thấy: Hbh ABCD cố định có G là trung điểm CD nên AG cố định. Mà I là trung điểm AG nên I cũng cố định.
Lại có: MN đi qua I nên MN luôn đi qua 1 điểm cố định (đpcm).
CM
12 tháng 12 2019
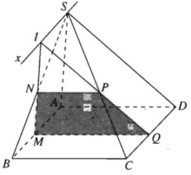
a) Vì M ∈ (SAB)
Và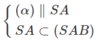 
nên (α) ∩ (SAB) = MN
và MN // SA
Vì N ∈ (SBC)
Và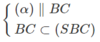 
nên (α) ∩ (SBC) = NP
và NP // BC (1)
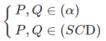⇒ (α) ∩ (SCD) = PQ
Q ∈ CD ⇒ Q ∈ (ABCD)
Và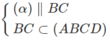 
nên (α) ∩ (ABCD) = QM
và QM // BC (2)
Từ (1) và (2) suy ra tứ giác MNPQ là hình thang.
b) Ta có:
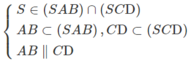⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
MN ∩ PQ = I ⇒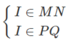 
MN ⊂ (SAB) ⇒ I ∈ (SAB), PQ ⊂ (SCD) ⇒ I ∈ (SCD)
⇒ I ∈ (SAB) ∩ (SCD) ⇒ I ∈ Sx
(SAB) và (SCD) cố định ⇒ Sx cố định ⇒ I thuộc Sx cố định.
Vì ABCD là hình bình hành => AB//CD mà AM thuộc AB; CN thuộc CD => AM//CN
Mà AM=CN
=> AMCN là hình bình hành (tứ giác có cặp cạnh đối // và = nhau là hình bình hành)
=> AC và MN là đường chéo của hbh AMCN
Gọi O là giao của AC và MN => O là trung điểm của AC và MN (Trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
A cố định C cố định => O cố định => MN luôn đi qua O cố định