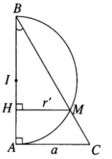
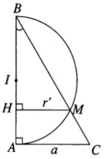
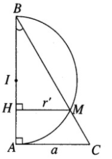
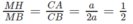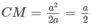Trong mặt phẳng \(\left(\alpha\right)\), cho tam giác ABC vuông tại A có cạnh AC = a và có cạnh huyền BC = 2a. Cũng trong mặt phẳng \(\left(\alpha\right)\) đó cho nửa đường tròn đường kính AB cẳ BC tại M
a) Chứng minh rằng khi quay mặt phẳng \(\left(\alpha\right)\) xung quanh AB có một mặt nón tròn xoay và một mặt cầu được tạo thành. Hãy xác định các mặt tròn xoay đó ?
b) Chứng minh rằng giao tuyến của hai mặt tròn xoay đó là một đường tròn. Hãy xác định bán kính của đường tròn đó ?
c) So sánh diện tích toàn phần của hình nón và diện tích của mặt cầu nói trên