Who help me

Câu E,F,G,H,I nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


dạng hướng dẫn tổng quát
A) hai tam giác cần c/m bằng nhau theo c.g.c
BA=AD=AC=AE và góc vuông A
b) Tương tự (a) b.1-Tam giác ADC và AEB {c.g.c}
có bốn cái cạnh (a) bằng nhau:
Góc đỉnh A bằng nhau đều =90 độ + góc BAC
p/s hai tam này bằng nhau và cân tại A
(b.2) hai tam giác = nhau theo (c.c.c)
có canh chung DE hai cái kia dùng kết quả của (a) và (b.1)
mỏi mắt quá. tạm thế


Xét tg MAB và tg MEC có:
M1 = M2 (đối đỉnh)
BM= MC ( M là trung điểm BC)
MA=ME (M là trung điểm AE)
=> Tg MAB = Tg MEC (cgc)
=> góc BAM = góc MEC
Mà 2 góc này ở vị trí slt => AB//CE
Góc BAC = 180-B1-C1
Góc C3=180 - C1-C2
Mà C2=B1 ( suy ra từ a)
=> góc BAC= góc C3
Xét tg ABC và tg CEG có:
góc BAC = góc C3 (CMT)
AB= CE
AC=CG ( vì C là trung điểm AG)
=> Tg ABC = tg CEG ( cgc)
=> góc C1= góc CGE
Mà 2 góc này ở vị trí đồng vị => BC // EG
Xét tg BME và tg CMA có:
góc M3 = góc M4 ( đối đỉnh)
MB = MC( M là trung điểm BC)
ME = AM ( M là trung điểm AE)
=> tg BME = tg CMA ( cgc)
=> EB = CA
góc B2 = C1
góc B3 = 180 - B1 - B2
C3= 180 - C2 - C1
Mà B1 = C2 ( suy từ câu a)
B2 = B1 ( cmt)
=> B3 = C3
Mà C3 = BAC
=> B3 = BAC
Xét Tg FBE và tg BAC có
góc B3= BAC ( cmt)
BF = AB ( B là trung điểm AF )
BE = AC
=> tg FBE = tg BAC ( cgc)
=> góc BFE = ABC
Mà 2 góc ở vị trí đồng vị
=> BC // FE (2)
Theo tiền đề Ơclit, từ ( 1) và (2) => EG trùng với FE
=> BC // FG
Hay F, E, G thẳng hàng

a: Xét tứ giác AEHF có
góc AEH=góc AFH=góc FAE=90 độ
nen AEHF là hình chữ nhật
b: Theo đề, ta có:
góc IAC+góc AFE=90 độ
=>góc IAC+góc AHE=90 độ
=>góc IAC+góc B=90 độ
mà góc C+góc B=90 độ
nên góc IAC=góc C
=>IA=IC và góc IAB=góc IBA
=>IA=IB=IC
=>I là trung điểm của BC

Xét \(\Delta EAF\) có :
AE = AF => \(\Delta EAF\) là tam giác cân
E = F = (180 - 80 ) : 2 = 50
=> E = F = 50
Xét \(\Delta ABC\) có :
B = C = (180 - 80 ) : 2 = 50
=> B = C = 50
=> E = B (=50)
=> EF // BC
Câu còn lại bạn tự làm nha
ý còn lại nè
\(\Delta ABC\) cân A nên AB=AC(1)
AE=AF(2)
E thuộc AB , F thuộc AC (3)
Từ (1)(2)(3)=> AB-AE=AC-AF
hay BF = CE

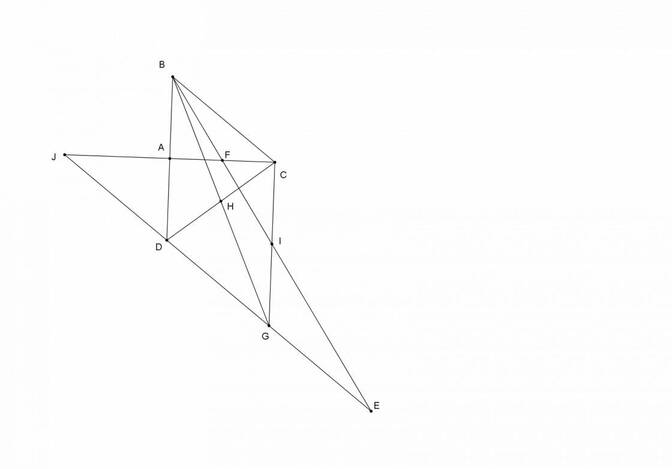
gọi $J$ là giao điểm của $DE,AC$, ta có $BCDJ $là hình thoi nên $BC\parallel JD$, $JA=AC=2CF\Rightarrow 3CF=JF$, theo Thales ta có \(\dfrac{BC}{EJ}=\dfrac{CF}{JF}=\dfrac{1}{3}\Rightarrow JE=3BC\), mà $JD=BC$ nên suy ra $DE=2BC$, hay $EG=DG=BC$, dẫn đến $BCEG,BCGD$ là hình bình hành, suy ra $H$ là trung điểm $CD,I$ là trung điểm $CG$, theo tính chất đường trung bình ta có \(IH=\dfrac{1}{2}DG=\dfrac{1}{4}DE\)
e: Ta có: \(E=\sqrt{19+8\sqrt{3}}-\sqrt{28-6\sqrt{3}}+\sqrt{12}\)
\(=4+\sqrt{3}-3\sqrt{3}+1+2\sqrt{3}\)
=5
còn các câu khác nữa ạ!