Có 2 cốc chứa nước trà tan có khối lượng m1 ở nhiệt độ t1=45 độ, cốc thứ hai chứa nước tinh khiết có khối lượng m2 ở nhiệt độ t2 = 5 độ. Để làm nguội nước trà trong cốc thư nhất, người ta đổ một khối lượng trà x từ cốc thứ nhất sang cốc thứ hai, sau khi khuấy đều cho cân bằng thì đổ lại cốc thứ nhất cũng một khối lượng x. Kết quả hiệu nhiệt độ ở 2 cốc là 15 độ. Còn nồng độ trà ở cốc thứ nhất gấp k= 2,5 lần cốc thứ hai. Tìm a1=x/m1 và a2=x/m2. Nếu tăng x thì sự chênh lệch nồng độ và nhiệt độ giữa 2 cốc sau khi pha tăng hay giảm? Trong bài toán này, khối lượng trà là nhỏ hơn so với khối lượng nước nên có thể coi khối lượng nước trà bằng khối lượng nước hòa tan trà, nước trà và nước có nhiệt rung riêng như nhau. Bỏ qua sự trao đổi nhiệt của nước, nước trà với cốc và với môi trường ngoài![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi n là nồng độ của trà 1 lúc ban đầu
\(n2=\dfrac{\Delta m.n}{\Delta m+m2}=\dfrac{n}{1+\dfrac{m2}{\Delta m}}\left(1\right)\)
thay \(x2=\dfrac{\Delta m}{m2}\)
thay vào trường hợp 1 ta có \(n2=\dfrac{n}{1+\dfrac{1}{x2}}=\dfrac{n.x2}{x2+1}\)
nếu trường hợp đổ trở lại m từ cốc 2 sang cốc 1thì nồng độ nước trà cốc 1
\(n1=\dfrac{\left(m1-\Delta m\right).n+\Delta m.n2}{\left(m1-\Delta m\right)+\Delta m}=\dfrac{\left(m1-\Delta m\right).n+\Delta m.\dfrac{n.x2}{x2+1}}{m1}=n-\dfrac{\Delta m.n}{m1}+\dfrac{\Delta m}{m1}.\dfrac{n.x2}{x2+1}\left(2\right)\)
thay \(x1=\dfrac{\Delta m}{m1}\)
vào trường hợp 2 ta có:\(n1=\left(1-x1\right).n+\dfrac{x1.x2.n}{x2+1}\)
theo giả thiết ta có:\(n1=k.n2\)
hay \(\left(1-x1\right).n+\dfrac{x1.x2.n}{x2+1}=k.\dfrac{n.x2}{x2+1}\)
\(1-x1=\dfrac{\left(k-x1\right).x2}{x2+1}\)
suy ra độ chênh lệch giữa hai cốc:\(k=\dfrac{\left(1-x1\right).\left(1+x2\right)}{x2}+x1=\dfrac{1+x2-x1-x1x2}{x2}+x1=\dfrac{1-x1}{x2}+1\left(3\right)\)
\(< =>\dfrac{1-x1}{x2}=k-1=2,5-1=1,5< =>1=1,5x2+x1\left(4\right)\)
khi đổ nước có khối lượng m từ bình 1 sang bình 2 ta có phương trình cân bằng nhiệt
m.c(t1-t)=m2.c(t-t2)
\(t=\dfrac{\Delta m.c.t1+m2.c.t2}{\Delta m.c+m2.c}=\dfrac{\Delta m.t1+m2.t2}{\Delta m+m2}\)
thêm bớt m2t1 vào tử ta có
\(t=\dfrac{\Delta m.t1+m2.t1+m2.t2-m2.t1}{\Delta m+m2}=t1+\dfrac{m2.\left(t2-t1\right)}{\Delta m+m2}=t1+\dfrac{t2-t1}{x2+1}=t1-\dfrac{t2-t1}{x2+1}\left(6\right)\)
khi đổ m trở lại cốc 1 ta có phương trình cân bằng nhiệt sau
m.c(t'-t)=(m1-m).c(t1-t')
\(=>t'=\dfrac{\Delta m.c.t+\left(m1-\Delta m\right)c.t1}{\Delta m.c\left(m1-\Delta m\right)c}=\dfrac{\Delta m.t+\left(m1-\Delta m\right).t1}{m1}< =>t'=x1.t+t1-x1.t1=x1\left(t-t1\right)+t1\)
thay vào trường hợp 6 ta có:\(t'=\left(t1-\dfrac{t1-t2}{x2+1}\right).x1+t1=t1-\dfrac{x1.\left(t1-t2\right)}{x2+1}\left(< >\right)\)
hiệu nhiệt độ giữa hai cốc
\(t=t'-t=t1-\dfrac{x1.\left(t1-t2\right)}{x2+1}-t1-\dfrac{t1-t2}{x2+1}=\dfrac{t1-t2-x1.\left(t1-t2\right)}{x2+1}=\dfrac{\left(1-x1\right).\left(t1-t2\right)}{x2+1}\left(\backslash\right)\)
thay t1,t2,t vào (/) ta có \(15=\dfrac{\left(1-x1\right).\left(45-5\right)}{x2+1}=>15x2+40x1=25\left(\backslash\backslash\right)\)
giải hệ phương trình từ (4) và (\\) ta có: ta được x1=\(\dfrac{1}{2}\)
x2=\(\dfrac{1}{3}\)
ta thấy khi m tăng thì \(x1=\dfrac{\Delta m}{m1}\)
x2=\(\dfrac{\Delta m}{m2}\)
đều tăng ,do đó từ phần (3) và (//) ta có k và t đều giảm

Đáp án: B
- Nhiệt lượng do cốc và nước toả ra để hạ nhiệt độ xuống 0 0 C là:
![]()
- Nhiệt lượng thu vào của khối nước đá để tăng nhiệt độ lên 0 0 C và tan hết tại 0 0 C là:
![]()
- Vì Q 1 > Q 2 nên khối nước đá đã tan hết và nhiệt độ hỗn hợp lớn hơn 0 0 C

Ta có: \(V_1=200cm^3\Rightarrow m_1=0,2kg,t_1=40^oC\)
\(V_2=800cm^3\Rightarrow m_2=0,8kg,t_2=90^oC\)
Nhiệt độ phòng chính là nhiệt độ cân bằng: \(t=20^oC\)
Nhiệt dung riêng của nước: \(c=4200\)
Nhiệt lượng thu vào của cốc nước ấm \(200cm^3\) là:
\(Q_1=m_1c\left(t_1-t\right)=0,2\cdot4200\cdot\left(40-20\right)=16800J\)
Nhiệt lượng thu vào của cốc nước ấm \(800cm^3\) là:
\(Q_2=m_2c\left(t_2-t\right)=0,8\cdot4200\cdot\left(90-20\right)=235200J\)
Cân bằng nhiệt ta đc:
\(Q_{tỏa}=Q_1+Q_2=252000\)
Nhiệt lượng nước đun sôi tỏa ra:
\(Q_{tỏa}=Q_3=m_3\cdot c\cdot\left(100-20\right)=252000J\)
\(\Rightarrow m_3=0,75kg\)
\(\Rightarrow V_3=750cm^3\)

Đáp án: B
Phương trình cân bằng nhiệt:
cm2(t2 – t) = lm1 + cm1t
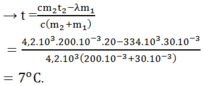

Đáp án: D
- Khi thả hai viên nước đá vào chậu nước. Giả sử nước đá tan hết ở 0 0 C .
- Nhiệt lượng do chậu và nước toả ra để hạ nhiệt độ xuống 0 0 C là:
Q 1 = ( m c + m 1 c 1 ) ( t 1 - 0 ) = 47000 ( J )
- Nhiệt lượng thu vào của 2 viên nước đá để tăng nhiệt độ lên 0 0 C và tan hết tại 0 0 C là:
Q 2 = 2 m 2 C 2 ( 0 - t 2 ) + 2 m 2 . λ = 13960 ( J )
- Vì Q 1 > Q 2 nên 2 viên đá sẽ tan hết và nhiệt độ cân bằng 0 0 C < t < 20 0 C .

Đáp án: A
- Nhiệt lượng do chậu và nước toả ra để hạ nhiệt độ xuống 0 0 C là:
![]()
- Nhiệt lượng thu vào của khối nước đá để tăng nhiệt độ lên 0 0 C và tan hết tại 0 0 C là:
![]()
- Vì Q 2 > Q 1 nên khối nước đá chưa tan hết

Giải kiểu này em chắc bn ấy ko thể hiểu được
Phải chia thành 4 cái Qthu: hóa hơi, tan chảy, từ -10 lên 0 độ, từ 0 độ lên 10 độ
1 cái Qthu: do nước tỏa nhiệt hạ từ 30->10 độ C

đoạn Qthu hơi nhầm lẫn xíu rối quá(bên dưới)
\(Qthu=170000M+\dfrac{1}{2}.2100.M.20+mC.20+2m.4200.20\)
\(=191000M+20mC+168000m\)
\(=>252000m+126000M=191000M+20mC+168000m\)
\(=>65000M=20m\left(4200-C\right)\left(2\right)\)
(2) chia(1)
\(=>\dfrac{260}{701}=\dfrac{2\left(4200-C\right)}{8401}=>C=...\)
đá chỉ tan một nửa nên nhiệt độ cuối cùng tcb=0oC
\(=>Qthu1=\dfrac{1}{2}M.34.10^4=170000M\left(J\right)\)
\(=>Qthu2=\dfrac{1}{2}M.2100.5=5250M\left(J\right)\)
\(=>Qtoa1=m.C.10=10m\left(J\right)\)
\(=>Qtoa2=2m.4200.10=84000m\left(J\right)\)
\(=>175250M=84010m\left(1\right)\)
khi rót một lượng nước ở t3=50oC
\(=>Qtoa=\left(2m+M\right).4200.\left(50-20\right)=\left(2m+M\right)126000\left(J\right)\)
\(=252000m+126000M\left(J\right)\)
\(=>Qthu=170000M+m.C.20+2m.4200.20\)
\(=170000M+20mC+168000m\left(J\right)\)
\(=>252000m+126000M=170000M+20mC+168000m\)
\(< =>\)\(44000M=20m\left(4100-C\right)\left(2\right)\)
(2) chia(1)
\(=>\dfrac{176}{701}=\dfrac{2\left(4100-C\right)}{8401}=>C=...\)
(bài này ko chắc , bạn bấm lại máy tính nhá , dài quá sợ sai)
