Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)(E)
Thay x=0 và y=-4 vào (E), ta được:
16/b^2=1
=>b=4
F2(3;0)
=>c=3
=>căn a^2-16=3
=>a^2-16=9
=>a=5
=>x^2/25+y^2/16=1
1: (E): x^2/a^2+y^2/b^2=1
Thay x=0 và y=3 vào (E), ta được:
3^2/b^2=1
=>b^2=9
=>b=3
F2(5;0)
=>c=5
=>\(\sqrt{a^2-9}=5\)
=>a^2-9=25
=>a^2=34
=>\(a=\sqrt{34}\)
=>x^2/34+y^2/9=1
2: Thay x=7 và y=0 vào (E), ta được:
7^2/a^2+0^2/b^2=0
=>a^2=49
=>a=7
Thay x=0 và y=3 vào (E), ta được:
0^2/a^2+3^2/b^2=1
=>b^2=9
=>b=3
=>(E): x^2/49+y^2/9=1
3: Thay x=0 và y=1 vào (E), ta được:
1/y^2=1
=>y=1
=>(E): x^2/a^2+y^2/1=1
Thay x=1 và y=căn 3/2 vào (E), ta được:
1^2/a^2+3/4=1
=>1/a^2=1/4
=>a^2=4
=>a=2
=>(E); x^2/4+y^2/1=1
a) (E) có tiêu điểm \({F_1}\left( { - \sqrt 3 ;0} \right)\) nên \(c = \sqrt 3\).
Phương trình chính tăc của (E) có dạng
\({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\)
Ta có: \(M\left( {1;{{\sqrt 3 } \over 2}} \right) \in (E)\)
\(\Rightarrow {1 \over {{a^2}}} + {3 \over {4{b^2}}} = 1\ (1)\)
Và \({a^2} = {b^2} + {c^2} = {b^2} + 3\)
Thay vào (1) ta được :
\(\eqalign{ & {1 \over {{b^2} + 3}} + {3 \over {4{b^2}}} = 1 \cr & \Leftrightarrow 4{b^2} + 3{b^2} + 9 = 4{b^2}(b + 3) \cr}\)
\(\Leftrightarrow 4{b^4} + 5{b^2} - 9 = 0 \Leftrightarrow {b^2} = 1\)
Suy ra \({a^2} = 4\)
Ta có a = 2 ; b = 1.
Vậy (E) có bốn đỉnh là : (-2 ; 0), (2 ; 0)
(0 ; -1) và (0 ; 1).
b) Phương trình chính tắc của (E) là :
\({{{x^2}} \over 4} + {{{y^2}} \over 1} = 1\)
c) (E) có tiêu điểm thứ hai là điểm \(\left( {\sqrt 3 ;0} \right)\). Đường thẳng \(\Delta\) đi qua điểm\(\left( {\sqrt 3 ;0} \right)\) và vuông góc với Ox có phương trình \(x = \sqrt 3\).
Phương trình tung độ giao điểm của \(\Delta\) và \((E)\) là :
\({3 \over 4} + {{{y^2}} \over 1} = 1 \Leftrightarrow {y^2} = \pm {1 \over 2}\)
Suy ra tọa độ của C và D là :
\(C\left( {\sqrt 3 ; - {1 \over 2}} \right)\) và \(\left( {\sqrt 3 ;{1 \over 2}} \right)\)
Vậy CD = 1.
F1(\(-\sqrt{3};0\)) => c=\(\sqrt{3}\)
có: \(b^2=a^2-c^2=a^2-3\)
pt elip di qua M:
\(\dfrac{3}{a^2}+\dfrac{1}{4b^2}=1\)
\(\Leftrightarrow\dfrac{3}{a^2}+\dfrac{1}{4a^2-12}=1\)
dat a^2=t (t>0)
\(\Leftrightarrow\dfrac{3}{t}+\dfrac{1}{4t-12}=1\\ \Leftrightarrow12t-36+t=4t^2-12t\)
\(\Leftrightarrow4t^2-25t+36=0\\ \Leftrightarrow\left[{}\begin{matrix}t=4\\t=\dfrac{9}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a^2=4\\a^2=\dfrac{9}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}b^2=1\\b^2=-\dfrac{3}{4}\left(loai\right)\end{matrix}\right.\)
=>ptelip: \(\dfrac{x^2}{4}+\dfrac{y^2}{1}=1\)
Đường thẳng Δ song song với d ⇒ Δ: x + y + c = 0, (c ≠ 0)
Vì Δ đi qua A ⇒ 3 + 0 + c = 0 ⇒ c = -3(tm)
Vậy đường thẳng Δ có dạng: x+y-3=0
Vì đường tròn có tâm I thuộc d nên I(a;-a)
Vì đường tròn đi qua A, B nên I A 2 = I B 2 ⇒ (3 - a ) 2 + a 2 = a 2 + (2 + a ) 2 ⇔ (3 - a ) 2 = (2 + a ) 2
Vậy phương trình đường tròn có dạng:
Ta có:
Giả sử elip (E) có dạng:
Vì (E) đi qua B nên:
Mà
Vậy phương trình chính tắc của elip (E) là:
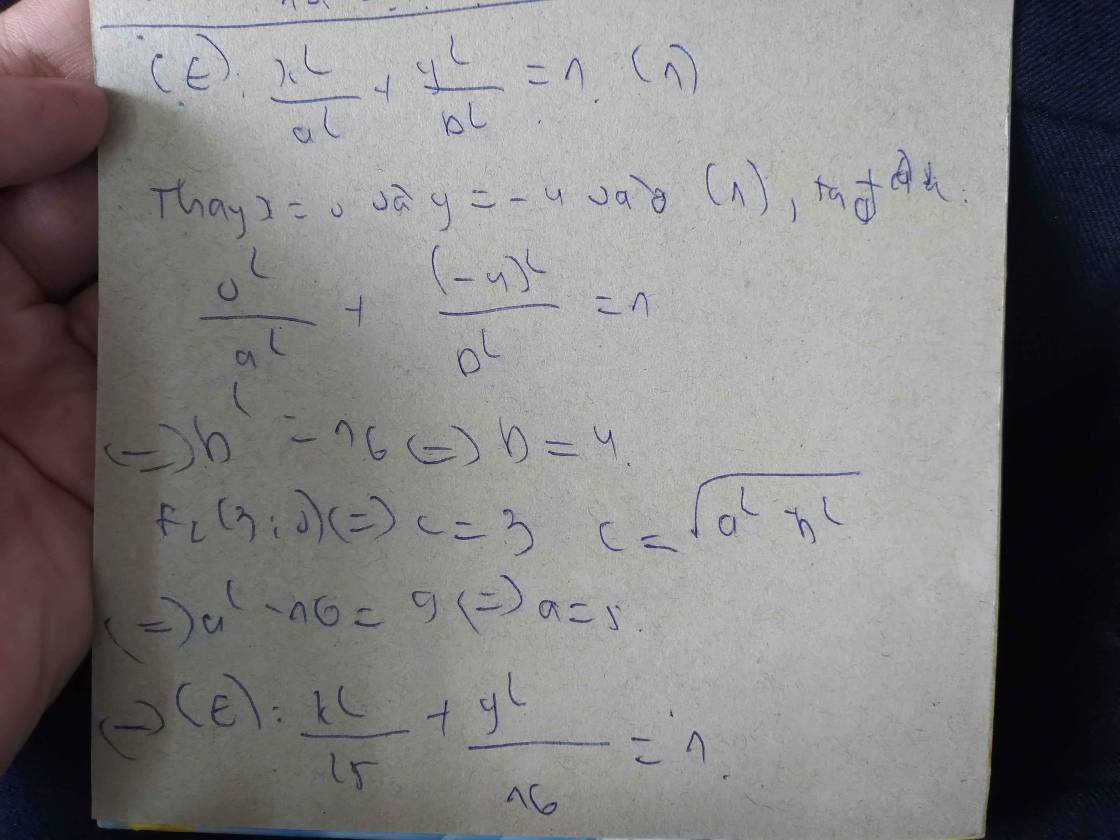
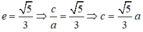
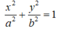
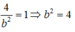
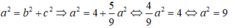
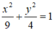
a, Phương trình chính tắc của (E) có dạng
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) với 0<b<a
Ta có A(0;2) \(\in\left(E\right)\)<=>b=2
(E) có tiêu điểm F1\(\left(-\sqrt{5};0\right)\) => c=\(\sqrt{5}\)
Ta có \(a^2=b^2+c^2=4+5=9\)=>a=3
==> (E) \(\dfrac{x^2}{9}+\dfrac{y^2}{4}=1\)
b, 2a = 6; 2b = 4; 2c = \(2\sqrt{5}\)=>\(\dfrac{c}{a}=\dfrac{\sqrt{5}}{3}\)
c, S=4ab=24