Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi \(A\left(x_A;y_A\right);B\left(x_B;y_B\right);C\left(x_C;y_C\right)\).
\(\overrightarrow{MN}\left(1;2\right)\); \(\overrightarrow{BP}\left(-x_B;-4-y_B\right)\).
MN là đường trung bình của tam giác ABC nên: \(\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{BC}=\overrightarrow{BN}\).
Vì vậy \(\left\{{}\begin{matrix}-x_B=1\\-4-y_B=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B=-1\\y_B=-6\end{matrix}\right.\)\(\Leftrightarrow B\left(-1;-6\right)\).
\(\overrightarrow{NP}\left(-2;-7\right)\); \(\overrightarrow{AM}\left(1-x_A;1-y_A\right)\).
NP là đường trung bình của tam giác ABC nên:
\(\overrightarrow{NP}=\dfrac{1}{2}\overrightarrow{AB}=\overrightarrow{AM}\).
Vì vậy \(\left\{{}\begin{matrix}1-x_A=-2\\1-y_A=-7\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_A=3\\y_A=8\end{matrix}\right.\)\(\Rightarrow A\left(3;8\right)\).
Do M là trung điểm của AB nên:
\(\dfrac{x_A+x_B}{2}=x_M\Rightarrow x_B=2x_M-x_A=2.1-3=-1\).
\(\dfrac{y_A+y_B}{2}=y_M\Rightarrow y_B=2y_M-y_A=2.1-8=-6\).
Vậy \(B\left(-1;-6\right)\).
bạn ơi, cách làm của bạn thì ok lắm nhưng theo mình thì có vẻ bạn đang nhầm đề bài á??... ví dụ ở đề bài M là trung điểm của BC nhưng trong hình vẽ của bạn điểm M lại là trung điểm của AB mất rồi!!! Đó là suy nghĩ của mình thoii, nếu như không hợp lý thì mình xin lỗi :))
a) Xác định các điểm –a, -b trên trục số:
b) Xác định các điểm |a|, |b|, |-a|, |-b| trên trục số:
c) So sánh các số a, b, -a, -b, |a|, |b|, |-a|, |-b| với 0:
a ở bên trái trục số => a là số nguyên âm nên a < 0.
Do đó: -a = |a| = |a| > 0.
b ở bên phải trục số => b là số nguyên dương nên b = |b| = |-b| > 0 và -b < 0.
Bài giải:
a) Xác định các điểm –a, -b trên trục số:
b) Xác định các điểm |a|, |b|, |-a|, |-b| trên trục số:
c) So sánh các số a, b, -a, -b, |a|, |b|, |-a|, |-b| với 0:
a ở bên trái trục số => a là số nguyên âm nên a < 0.
Do đó: -a = |a| = |a| > 0.
b ở bên phải trục số => b là số nguyên dương nên b = |b| = |-b| > 0 và -b < 0.
- Xét phương trình hoành độ của (P) với Ox : \(\Rightarrow\left\{{}\begin{matrix}OA\left(\dfrac{4}{3};0\right)\\OB\left(-1;0\right)\end{matrix}\right.\)
- Từ đồ thị hàm số \(\Rightarrow S_{ABMN}=\dfrac{1}{2}\left(\left|AB\right|+\left|MN\right|\right).\left|m\right|=4\)
\(\Rightarrow\left(\dfrac{7}{3}+\left|MN\right|\right).\left(-m\right)=8\)
\(\Rightarrow\left|MN\right|=-\dfrac{8}{m}-\dfrac{7}{3}\)
\(\Rightarrow MN^2=\dfrac{64}{m^2}+\dfrac{112}{3m}+\dfrac{49}{9}\)
- Xét phương trình hoành độ giao điểm (P) và d :\(3x^2-x-m-4=0\)
Có : \(\Delta=b^2-4ac=1-4.3\left(-m-4\right)=12m+49\)
- Để P cắt d tại hai điểm phân biệt <=> \(m>-\dfrac{49}{12}\)
\(\Rightarrow-\dfrac{49}{12}< m< 0\)
- Theo vi ét : \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{1}{3}\\x_1x_2=-\dfrac{m+4}{3}\end{matrix}\right.\)
Thấy : \(\left|MN\right|=\left|x_1\right|+\left|x_2\right|\)
\(\Rightarrow MN^2=x^2_1+2\left|x_1x_2\right|+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2+2\left|x_1x_2\right|\)
\(\Rightarrow\dfrac{2\left(m+4\right)}{3}+\dfrac{2}{3}\left|m+4\right|=\dfrac{64}{m^2}+\dfrac{112}{3m}+\dfrac{16}{3}\)
TH1 : \(m+4< 0\)
\(\Rightarrow16m^2+112m+192=0\)
\(\Rightarrow\left[{}\begin{matrix}m=-3\\m=-4\end{matrix}\right.\)
TH2 : \(m+4\ge0\)
\(\Rightarrow\dfrac{4\left(m+4\right)m^2}{3m^2}=\dfrac{16m^2+112m+192}{3m^2}\)
\(\Rightarrow4m^3-112m-192=0\)
( Đoạn này giải máy nha cho nhanh nếu ko tách đc bl để mk tách cho )
\(\Rightarrow\left[{}\begin{matrix}m=-2\\m=-4\end{matrix}\right.\)
Vậy ...
Ta có : \(y'\left(x\right)=4mx^3+\left(6m+\frac{1}{12}\right)x\)
Ta có hệ số góc các tiếp tuyến \(\left(C_m\right)\) tại A và B lần lượt là :
\(y'\left(-1\right)=-10m-\frac{1}{12}\) và \(y'\left(2\right)=44m+\frac{1}{6}\)
Do đó các tiếp tuyến của \(\left(C_m\right)\) tại A và B vuông góc với nhau khi và chỉ khi :
\(y'\left(-1\right).y'\left(2\right)=-1\Leftrightarrow\left(-10m-\frac{1}{12}\right)\left(44m+\frac{1}{6}\right)=-1\)
\(\Leftrightarrow440m^2+\frac{16}{3}m-\frac{71}{72}=0\Leftrightarrow\left[\begin{array}{nghiempt}m=\frac{1}{24}\\m=-\frac{71}{1320}\end{array}\right.\)
Vậy giá trị cần tìm là \(\begin{cases}m=\frac{1}{24}\\m=-\frac{71}{1320}\end{cases}\)
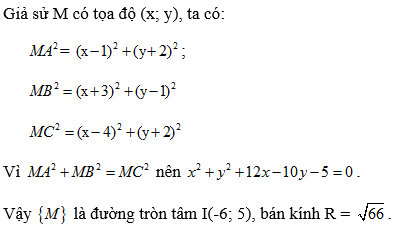
a)Do A',B',C' là trung điểm BC,CA,AB=> A'B' song song với AB,B'C'song song với BC,C'A' song song với CA
\(\overrightarrow{A'B'}=\left(6;3\right)\) => VTPT của đường thẳng AB là: \(\overrightarrow{n}=\left(1;-2\right)\)
và C' thuộc (AB)=>Phương trình đường thẳng AB là:
(AB): x-2y-6=0
Tương tự ta có phương trình đường thẳng BC là:
(BC): x+4=0
Tọa độ điểm B là nghiệm hệ
\(\left\{{}\begin{matrix}\text{x-2y-6=0}\\x+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=-5\end{matrix}\right.\)
=>B(-4;-5)
A'(-4;1) là TĐ của BC => tọa độ C(-4;7)
C'(2;-2) là TĐ của AB =>tọa độ A(8;1)
b) Gọi tọa độ trọng tâm G của tam giác A'B'C' là G(x;y)
=>\(\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}=0\)
=>\(\left\{{}\begin{matrix}\left(-4-x\right)+\left(2-x\right)+\left(2-x\right)=0\\\left(1-y\right)+\left(4-y\right)+\left(-2-y\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
=>G(0;1)
Thay vào tính
Ta có:\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\) =(8-4-4;1-1+7-1-5-1)=(0;0)
=>G là trọng tâm tam giác ABC=>ĐPCM