Tính B = \(\dfrac{1}{6}+\dfrac{1}{24}+\dfrac{1}{60}+.......+\dfrac{1}{990}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BX
1
5 tháng 2 2023
\(2.B=\dfrac{2}{6}+\dfrac{2}{14}+\dfrac{2}{60}+...+\dfrac{2}{990}\)
\(2B=\dfrac{2}{1.2.3}+\dfrac{2}{2.3.4}+...+\dfrac{2}{9.10.11}\)
\(2B=\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+\dfrac{1}{3.4}-\dfrac{1}{4.5}+...+\dfrac{1}{9.10}-\dfrac{1}{10.11}\)
\(2B=\dfrac{1}{1.2}-\dfrac{1}{10.11}\)
\(B=\dfrac{27}{110}\)
10 tháng 5 2017
a, \(1\dfrac{13}{15}.\left(0,5\right)^2.3+\left(\dfrac{8}{15}-1\dfrac{19}{60}\right):1\dfrac{23}{24}\)
= \(\dfrac{28}{15}.\dfrac{25}{100}.3+\left(\dfrac{8}{15}-\dfrac{79}{60}\right):\dfrac{47}{24}\)
= \(\dfrac{28}{15}.\dfrac{1}{4}.3+\left(\dfrac{32-79}{60}\right).\dfrac{24}{47}\)
= \(\dfrac{84}{60}+\dfrac{-47}{60}.\dfrac{24}{47}\)
= \(\dfrac{84}{60}+\dfrac{-24}{60}=\dfrac{60}{60}=1\)
b, \(\dfrac{\left(\dfrac{11^2}{200}+0,415\right):0,01}{\dfrac{1}{12}-37,25+3\dfrac{1}{6}}\)
= \(\dfrac{\left(\dfrac{121}{200}+\dfrac{415}{1000}\right):\dfrac{1}{100}}{\dfrac{1}{12}-\dfrac{3725}{100}+\dfrac{19}{6}}=\dfrac{\left(\dfrac{121}{200}+\dfrac{83}{200}\right).100}{\dfrac{1}{12}-\dfrac{149}{4}+\dfrac{19}{6}}\)
= \(\dfrac{\dfrac{51}{50}.100}{-34}=\dfrac{102}{-34}=-3\)
KH
8 tháng 6 2021
\(1\dfrac{13}{15}\cdot\left(0,5\right)^2+3\cdot\left(\dfrac{8}{15}+1\dfrac{19}{60}\right):1\dfrac{23}{24}\)
\(=\dfrac{28}{15}\cdot\dfrac{1}{4}+3\cdot\left(\dfrac{8}{15}+\dfrac{79}{60}\right):\dfrac{47}{24}\)
\(=\dfrac{7}{15}+3\cdot\dfrac{37}{20}\cdot\dfrac{24}{47}\)
\(=\dfrac{7}{15}+\dfrac{666}{235}=\dfrac{2327}{705}\)
9 tháng 6 2021
\(1\dfrac{13}{15}.\left(0,5\right)^2+3.\left(\dfrac{8}{15}+1\dfrac{19}{60}\right):1\dfrac{23}{24}\)
\(=\dfrac{28}{15}.\dfrac{1}{4}+3.\left(\dfrac{8}{15}+\dfrac{79}{60}\right):\dfrac{47}{24}\)
\(=\dfrac{7}{15}+3.\dfrac{37}{20}:\dfrac{47}{24}\)
\(=\dfrac{7}{15}+\dfrac{666}{235}\)
\(=\dfrac{2327}{705}\)
MT
7 tháng 5 2021
A= 1/3+1/6+1/12+1/24+1/48+1/96
= (1/3+1/6)+(1/12+1/24)+(1/48+1/96)
= (2/6+1/6)+(2/24+1/24)+(2/96+1/96)
= 1/2+1/8+1/32
= 16/32+4/32+1/32
= 21/32
Vậy A=21/32
7 tháng 5 2021
Giải:
A=1/3+1/6+1/12+1/24+1/48+1/96
A=1/3+(1/2.3+1/3.4)+(1/4.6+1/6.8)+1/96
A=1/3+(1/2-1/3+1/3-1/4)+[1/2.(2/4.6+2/6.8)]+1/96
A=1/3+(1/2-1/4)+[1/2.(1/4-1/6+1/6-1/8)]+1/96
A=1/3+1/4+[1/2.(1/4-1/8)]+1/96
A=1/3+1/4+[1/2.1/8]+1/96
A=1/3+1/4+1/16+1/96
A=7/12+7/96
A=21/32
NN
2
24 tháng 4 2017
\(B=\dfrac{1}{18}+\dfrac{1}{54}+...+\dfrac{1}{990}\)
\(\Rightarrow B=\dfrac{1}{3.6}+\dfrac{1}{6.9}+...+\dfrac{1}{30.33}\)
\(\Rightarrow B=\dfrac{1}{3}\left(\dfrac{3}{3.6}+\dfrac{3}{6.9}+...+\dfrac{3}{30.33}\right)\)
\(\Rightarrow B=\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{9}+...+\dfrac{1}{30}-\dfrac{1}{33}\right)\)
\(\Rightarrow B=\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{33}\right)\)
\(\Rightarrow B=\dfrac{1}{3}.\dfrac{10}{33}\)
\(\Rightarrow B=\dfrac{10}{99}\)
Vậy...
24 tháng 4 2017
\(B=\dfrac{1}{18}+\dfrac{1}{54}+\dfrac{1}{108}+...+\dfrac{1}{990}\)
\(\Leftrightarrow B=\dfrac{1}{3.6}+\dfrac{1}{6.9}+\dfrac{1}{9.12}+..+\dfrac{1}{30.33}\)
\(\Leftrightarrow B=\left(\dfrac{1}{3}-\dfrac{1}{6}\right)+\left(\dfrac{1}{6}-\dfrac{1}{9}\right)+...+\left(\dfrac{1}{30}-\dfrac{1}{33}\right)\)
\(\Leftrightarrow B=\dfrac{1}{3}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{9}+\dfrac{1}{9}-...+\dfrac{1}{30}-\dfrac{1}{33}\)
\(\Leftrightarrow B=\dfrac{1}{3}-\dfrac{1}{33}\)
\(\Leftrightarrow B=\dfrac{10}{33}\).
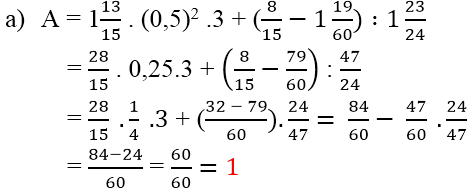
Ta có:\(B=\dfrac{1}{6}+\dfrac{1}{24}+\dfrac{1}{60}+...+\dfrac{1}{990}\)
\(2B=\dfrac{2}{6}+\dfrac{2}{24}+\dfrac{2}{60}+...+\dfrac{2}{990}\)
\(2B=\dfrac{2}{1\cdot2\cdot3}+\dfrac{2}{2\cdot3\cdot4}+\dfrac{2}{3\cdot4\cdot5}+...+\dfrac{2}{9\cdot10\cdot11}\)
\(2B=\dfrac{1}{1\cdot2}-\dfrac{1}{2\cdot3}+\dfrac{1}{2\cdot3}-\dfrac{1}{3\cdot4}+\dfrac{1}{3\cdot4}-\dfrac{1}{4\cdot5}+...+\dfrac{1}{9\cdot10}-\dfrac{1}{10\cdot11}\)
\(2B=\dfrac{1}{1\cdot2}-\dfrac{1}{10\cdot11}\)
\(2B=\dfrac{27}{55}\)
\(B=\dfrac{27}{55}:2\)
\(B=\dfrac{27}{110}\)