Cho hình thang cân ABCD có đáy nhỏ AB = AD. Biết \(\tan\widehat{BDC}=\dfrac{3}{4}\). Tính các giá trị lượng giác của \(\widehat{BAD}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

30 tháng 9 2018
ấn vào câu hỏi tương tự ấy
https://olm.vn/hoi-dap/question/1004845.html
GN
0


24 tháng 7 2021
Bài 2:
a) Xét ΔABC có
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\left(AM=AN;AB=AC\right)\)
Do đó: MN//BC(Định lí Ta lét đảo)
Xét tứ giác BMNC có MN//BC(gt)
nên BMNC là hình thang có hai đáy là MN và BC(Định nghĩa hình thang)
Hình thang BMNC có \(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
nên BMNC là hình thang cân(Dấu hiệu nhận biết hình thang cân)
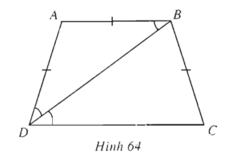
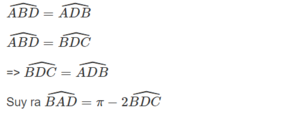
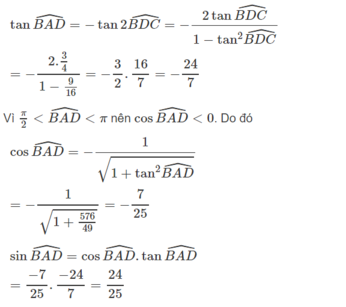
Ta có :
\(\widehat{ABD}=\widehat{ADB}\)
\(\widehat{ABD}=\widehat{BDC}\)
\(\Rightarrow\widehat{BDC}=\widehat{ADB}\)
Suy ra \(\widehat{BAD}=\pi-2\widehat{BDC}\)
Từ đó ta có :
\(\tan\widehat{BAD}=-\tan2\widehat{BDC}=-\dfrac{2\tan\widehat{BDC}}{1-\tan^2\widehat{BDC}}=-\dfrac{2.\dfrac{3}{4}}{1-9\cdot16}=-\dfrac{3}{2}.\dfrac{16}{7}=-\dfrac{24}{7}\)Vì \(\dfrac{\pi}{2}< \widehat{BAD}< \pi\) nên \(\cos\widehat{BAD}< 0\)
Do đó : \(\cos\widehat{BAD}=-\dfrac{1}{\sqrt{1+\tan^2\widehat{BAD}}}=-\dfrac{1}{\sqrt{1+\dfrac{576}{49}}}=-\dfrac{7}{25}\)
\(\sin\widehat{BAD}=\cos\widehat{BAD}\tan\widehat{BAD}=\dfrac{-7}{25}.\dfrac{-24}{7}=\dfrac{24}{25}\)