Cho tam giác ABC , trên AC lấy E , qua E kẻ ED , EF lần lượt song song với BC , AB ( D thuộc AB , F thuộc BC ) . Biết diện tích tam giác ADE là 101 cm2 và diện tích tam giác EFC là 143 cm2 , tính diện tích tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
11 tháng 12 2019
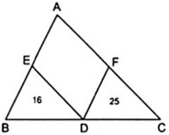
Đặt S A B C = S . Vì DE//AC nên Δ BED ∼ Δ BAC
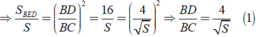
Lại có DF//AB nên Δ CDF ∼ Δ CBA
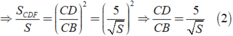
Cộng theo vế của đẳng thức ( 1 ) và ( 2 ) ta được:
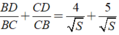
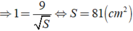
Vậy diện tích của tam giác ABC là 81 c m 2
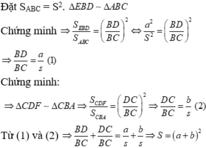
+) ED // BF; FE // BD => Tứ giác FBDE là hbh => DE = BF
+) Dễ có: tam giác ADE đồng dạng với ABC => \(\frac{S_{ADE}}{S_{ABC}}=\left(\frac{DE}{BC}\right)^2\) (*) ( tỉ số diện tích = bình phương tỉ số đồng dạng)
Tam giác CFE đồng dạng với tam giác CAB => \(\frac{S_{CFE}}{S_{ABC}}=\left(\frac{CF}{BC}\right)^2\)
=> \(\frac{S_{ADE}}{S_{ABC}}:\frac{S_{CFE}}{S_{ABC}}=\left(\frac{DE}{BC}\right)^2:\left(\frac{CF}{CB}\right)^2\) => \(\frac{S_{ADE}}{S_{CFE}}=\left(\frac{DE}{FC}\right)^2=\frac{101}{143}\) => \(\left(\frac{BF}{CF}\right)^2=\frac{101}{143}\)
=> \(\frac{BF}{CF}=\sqrt{\frac{101}{143}}\) => \(\frac{BF}{CF+BF}=\frac{\sqrt{101}}{\sqrt{143}+\sqrt{101}}\)=> \(\frac{BF}{BC}=\frac{\sqrt{101}}{\sqrt{143}+\sqrt{101}}=\frac{DE}{BC}\)
Thay vào (*) => \(\frac{S_{ADE}}{S_{ABC}}=\left(\frac{\sqrt{101}}{\sqrt{101}+\sqrt{143}}\right)^2=\frac{101}{S_{ABC}}\) => S(ABC) =....
Câu này là của Ai Lê hay Quỳnh ?