xin mn đừng lm tắt
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 8 2021
a: Ta có: \(2x+3=x+1\)
\(\Leftrightarrow2x-x=1-3\)
hay x=-2
b: Ta có: \(2x\left(2x-1\right)-\left(2x+3\right)^2=5\)
\(\Leftrightarrow4x^2-2x-4x^2-12x-9=5\)
\(\Leftrightarrow-14x=14\)
hay x=-1
c: Ta có: \(4x^2-25\left(x+2\right)^2=0\)
\(\Leftrightarrow\left(2x-5x-10\right)\left(2x+5x+10\right)=0\)
\(\Leftrightarrow\left(-3x-10\right)\left(7x+10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-10}{3}\\x=-\dfrac{10}{7}\end{matrix}\right.\)
16 tháng 8 2021
d: Ta có: \(2x^2+7x+5=0\)
\(\Leftrightarrow\left(x+1\right)\left(2x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{5}{2}\end{matrix}\right.\)
e: Ta có: \(4x^2-4x=-1\)
\(\Leftrightarrow4x^2-4x+1=0\)
\(\Leftrightarrow2x-1=0\)
hay \(x=\dfrac{1}{2}\)
f: Ta có: \(\dfrac{1}{9}x^3-x=0\)
\(\Leftrightarrow x\left(\dfrac{1}{9}x^2-1\right)=0\)
\(\Leftrightarrow x\left(\dfrac{1}{3}x-1\right)\left(\dfrac{1}{3}x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\)
g: Ta có: \(x^3+3x^2+3x=7\)
\(\Leftrightarrow\left(x+1\right)^3=8\)
\(\Leftrightarrow x+1=2\)
hay x=1
20 tháng 8 2021
1) \(x^3-8x+7=\left(x-1\right)\left(x^2+x-7\right)\)
2) \(x^3+8x^2-9=\left(x-1\right)\left(x^2+9x+9\right)\)
3) \(3x^3-4x+1=\left(x-1\right)\left(3x^2+3x-1\right)\)
4) \(x^4-3x^2+3x-1=\left(x-1\right)\left(x^3+x^2-2x+1\right)\)
5) \(x^4-5x^2+4=\left(x-1\right)\left(x-2\right)\left(x+1\right)\left(x+2\right)\)
20 tháng 8 2021
1: Ta có: \(x^3-8x+7\)
\(=x^3-x-7x+7\)
\(=x\left(x-1\right)\left(x+1\right)-7\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2+x-7\right)\)
2: Ta có: \(x^3+8x^2-9\)
\(=x^3-x^2+9x^2-9\)
\(=x^2\left(x-1\right)+9\left(x-1\right)\left(x+1\right)\)
\(=\left(x-1\right)\left(x^2+9x+9\right)\)
3: Ta có: \(3x^3-4x+1\)
\(=3x^3-3x-x+1\)
\(=3x\left(x-1\right)\left(x+1\right)-\left(x-1\right)\)
\(=\left(x-1\right)\left(3x^2+3x-1\right)\)
4: Ta có: \(x^4-3x^2+3x-1\)
\(=\left(x-1\right)\left(x+1\right)\left(x^2+1\right)-3x\cdot\left(x-1\right)\)
\(=\left(x-1\right)\cdot\left(x^3+x+x^2+1-3x\right)\)
\(=\left(x-1\right)\left(x^3+x^2-2x+1\right)\)
18 tháng 10 2021
b: Ta có: \(x\left(x+1\right)-\left(2x+3\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-2x-3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-1\end{matrix}\right.\)
d: Ta có: \(\left(x-1\right)^2-4\left(x+2\right)^2=0\)
\(\Leftrightarrow\left(x-1-2x-4\right)\left(x-1+2x+4\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(3x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-1\end{matrix}\right.\)
18 tháng 10 2021
a: \(x^2-4x-5=\left(x-5\right)\left(x+1\right)\)
b: \(x^2-3x+2=\left(x-2\right)\left(x-1\right)\)
d: \(2x^2-3x+1=\left(x-1\right)\left(2x-1\right)\)
k: \(4x^2-9=\left(2x-3\right)\left(2x+3\right)\)
DC
16 tháng 3 2022
câu 2 :
\(\dfrac{-55}{132}=\dfrac{\left(-55\right):12}{132:12}=\dfrac{-5}{12}\)
câu 3:
a) < b) <
câu 4 :
a)\(\dfrac{5}{16}-\dfrac{5}{24}=\dfrac{5}{48}\)
b) \(\dfrac{-5}{8}+\dfrac{12}{7}+\dfrac{13}{8}+\dfrac{2}{7}=\left(\dfrac{-5}{8}+\dfrac{13}{8}\right)+\left(\dfrac{12}{7}+\dfrac{2}{7}\right)=1+2=3\)
VP
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 11 2021
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
\(\Leftrightarrow2x-2\sqrt{2x^2+5x-3}=1+x\left(\sqrt{2x-1}-2\sqrt{x+3}\right)\)
\(\Leftrightarrow2x-1-2\sqrt{\left(2x-1\right)\left(x+3\right)}-x\left(\sqrt{2x-1}-2\sqrt{x+3}\right)=0\)
\(\Leftrightarrow\sqrt{2x-1}\left(\sqrt{2x-1}-2\sqrt{x+3}\right)-x\left(\sqrt{2x-1}-2\sqrt{x+3}\right)=0\)
\(\Leftrightarrow\left(\sqrt{2x-1}-x\right)\left(\sqrt{2x-1}-2\sqrt{x+3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2x-1}=x\left(x\ge0\right)\\\sqrt{2x-1}=2\sqrt{x+3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x-1=x^2\\2x-1=4\left(x+3\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{13}{2}\left(loại\right)\end{matrix}\right.\)
DT
3
8 tháng 11 2021
Bài 3:
a. \(R=p\dfrac{l}{S}=1,1.10^{-6}\dfrac{30}{0,2.10^{-6}}=165\Omega\)
b. \(Q=UIt=220\left(\dfrac{220}{165}\right).15.60=254000\left(J\right)\)
8 tháng 11 2021
Bài 2:
a. \(R=\dfrac{U^2}{P}=\dfrac{220^2}{1000}=48,4\Omega\)
b. \(Q=UIt=220\left(\dfrac{220}{48,4}\right).4.3600=14400000\left(J\right)\)
c. \(Q'=Q.40=14400000.40=576000000\left(J\right)=120000\)kWh
\(\Rightarrow T=Q'.2100=120000.2100=252000000\left(dong\right)\)
5 tháng 8 2021
2) Tìm x:
a) \(x^2+5x+6=0\)
⇒\(x^2+2x+3x+6=0\)
⇒\(\left(x^2+2x\right)+\left(3x+6\right)=0\)
⇒\(\left(x.x+2.x\right)+\left(3.x+3.2\right)=0\)
⇒\(x.\left(x+2\right)+3.\left(x+2\right)=0\)
⇒\(\left(x+2\right).\left(x+3\right)=0\)
⇒\(x+2=0\) \(hoặc\) \(x+3=0\)
\(+\))\(x+2=0\) \(+\))\(x+3=0\)
⇔\(x=-2\) ⇔\(x=-3\)
\(Vậy\) \(x\in\left\{-3;-2\right\}\)
c)\(x^2+6x+8=0\)
⇒ \(x^2+4x+2x+8=0\)
⇒ \(\left(x^2+4x\right)+\left(2x+8\right)=0\)
⇒ \(\left(x.x+4.x\right)+\left(2.x+2.4\right)=0\)
⇒ \(x.\left(x+4\right)+2.\left(x+4\right)=0\)
⇒ \(\left(x+4\right).\left(x+2\right)=0\)
⇒\(x+4=0\) \(hoặc\) \(x+2=0\)
\(+\)) \(x+4=0\) \(+\)) \(x+2=0\)
⇔\(x=-4\) ⇔\(x=-2\)
\(Vậy\) \(x\in\left\{-4;-2\right\}\)
5 tháng 8 2021
a) x2+5x+6=0
⇒x2+2x+3x+6=0
⇒(x2+2x)+(3x+6)=0
⇒x(x+2)+3(x+2)=0
⇒(x+2)(x+3)=0
\(\Rightarrow\left[{}\begin{matrix}x+2=0\\x+3=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-2\\x=-3\end{matrix}\right.\)
b) 9x3=x
⇒9x3-x=0
⇒9x(x2-1)=0
⇒\(\left[{}\begin{matrix}9x=0\\x^2-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x^2=1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=\pm1\end{matrix}\right.\)
c) x2+6x+8=0
⇒ x2+2x+4x+8=0
⇒ (x2+2x)+(4x+8)=0
⇒ x(x+2)+4(x+2)=0
⇒ (x+2)(x+4)=0
\(\Rightarrow\left[{}\begin{matrix}x+2=0\\x+4=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-2\\x=-4\end{matrix}\right.\)
d) x(x-3)-(x-2)2=x+1
⇒x2-3x-x2+4x-4=x+1
⇒x2-3x-x2+4x-4-x-1=0
⇒-5=0(vô lí)
e) (x+2)(x+3)-(x+1)2=0
⇒x2+5x+6-x2-2x-1=0
⇒3x+5=0
⇒3x=-5
⇒x=\(-\dfrac{5}{3}\)
f)x(x+1)-(x+1)2=0
⇒(x-x-1)(x+1)=0
⇒-1(x+1)=0
⇒x+1=0
⇒x=-1
g) (x-2)2-4(x+3)2=0
⇒x2-4x+4-4(x2+6x+9)=0
⇒x2-4x+4-4x2-24x-36=0
⇒-3x2-28x-32=0
đến đây mik chx bt lm
8 tháng 1 2022
\(\Leftrightarrow x^2-12x+36-x^2+10x=40\)
=>-2x=4
hay x=-2
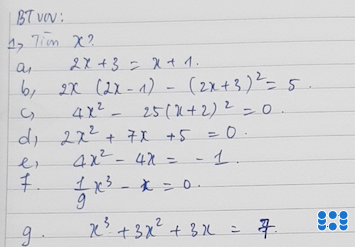
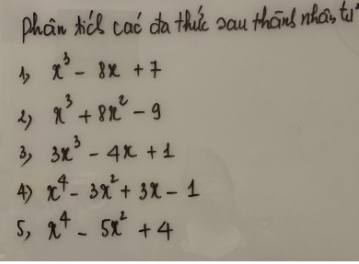
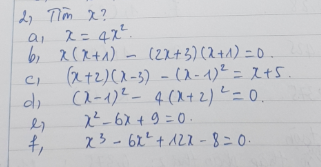
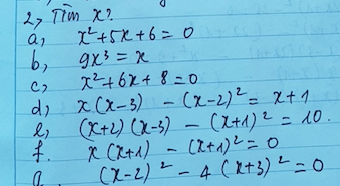
\(a,4x^2-6x=2x\left(2x-3\right)\\ b,9x^4y^3+3x^2y^4=3x^2y^3\left(2x^2+y\right)\\ c,x^3-2x^2+5x=x\left(x^2-2x+5\right)\\ d,3x\left(x-1\right)+5\left(x-1\right)=\left(3x+5\right)\left(x-1\right)\\ e,2x^2\left(x+1\right)+4\left(x+1\right)=\left(x+1\right)\left(2x^2+4\right)=2\left(x+1\right)\left(x^2+2\right)\\ f,2x^2y-4xy^2+6xy=2xy\left(x-y+3\right)\\ g,4x^3+4x^2+4x=4x\left(x^2+x+1\right)\\ h,x^3+x^2-3x-27=x^3-3x^2+4x^2-12x+9x-27=x^2\left(x-3\right)+4x\left(x-3\right)+9\left(x-3\right)=\left(x^2+4x+9\right)\left(x-3\right)\\ i,4x^2-12x+9=\left(2x-3\right)^2\\ k,8x^3-27=\left(2x\right)^3-3^3=\left(2x-3\right)\left(4x^2+6x+9\right)\\ l,x^2+6x+5=x^2+x+5x+5=x\left(x+1\right)+5\left(x+1\right)=\left(x+1\right)\left(x+5\right)\)
Tick nha 😘
Đây nè bạn đã cố gắng ko làm tắt rồi nhé bạn