Chứng minh rằng với \(n\in N^{\circledast}\), ta có :
a) \(n^3+3n^2+5n\) chia hết cho 3
b) \(4^n+15n-1\) chia hết cho 9
c) \(n^3+11n\) chia hết cho 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đặt Sn = n3 + 3n2 + 5n
Với n = 1 thì S1 = 9 chia hết cho 3
Giả sử với n = k ≥ 1, ta có Sk = (k3 + 3k2 + 5k) 3
Ta phải chứng minh rằng Sk+1 3
Thật vậy Sk+1 = (k + 1)3 + 3(k + 1)2 + 5(k + 1)
= k3 + 3k2 + 3k + 1 + 3k2 + 6k + 3 + 5k + 5
= k3 + 3k2 + 5k + 3k2 + 9k + 9
hay Sk+1 = Sk + 3(k2 + 3k + 3)
Theo giả thiết quy nạp thì Sk 3, mặt khác 3(k2 + 3k + 3)
3 nên Sk+1
3.
Vậy (n3 + 3n2 + 5n) 3 với mọi n ε N* .
b) Đặt Sn = 4n + 15n - 1
Với n = 1, S1 = 41 + 15.1 – 1 = 18 nên S1 9
Giả sử với n = k ≥ 1 thì Sk= 4k + 15k - 1 chia hết cho 9.
Ta phải chứng minh Sk+1 9.
Thật vậy, ta có: Sk+1 = 4k + 1 + 15(k + 1) – 1
= 4(4k + 15k – 1) – 45k + 18 = 4Sk – 9(5k – 2)
Theo giả thiết quy nạp thì Sk 9 nên 4S1
9, mặt khác 9(5k - 2)
9, nên Sk+1
9
Vậy (4n + 15n - 1) 9 với mọi n ε N*

a)Đặt \(E_n=n^3+3n^2+5n\)
\(E_k=k^3+3k^2+5k\) chia hết 3 (giả thiết quy nạp)
Ek+1=(k+1)3+3(k+1)2+5(k+1) chia hết 3
Thật vậy:
Ek+1=(k+1)3+3(k+1)2+5(k+1)
=k3+3k2+5k+3k2+9k+9=Ek+3(k2+3k+3)
Theo giả thiết quy nạp thì Ek chia hết 3
ngoài ra 3(k2+3k+3) chia hết 3 nên Ek chia hết 3
=>Ek chia hết 3 với mọi \(n\in N\)*

a) Với n = 1, ta có:
13n – 1 = 131 – 1 = 12 ⋮ 6
Giả sử: 13k - 1 ⋮ 6 với mọi k ≥ 1
Ta chứng minh: 13k+1 – 1 chia hết cho 6
Thật vậy:
13k+1 – 1 = 13k+1 – 13k+ 13k -1 = 12.13k +13k – 1
Vì : 12.13k ⋮ 6 và 13k – 1 ⋮ 6
Nên : 13k+1 – 1 ⋮ 6
Vậy 13n -1 chia hết cho 6
b) Với n = 1, ta có: 3n3 + 15n = 18 ⋮ 9
Giả sử: 3(k + 1)3 + 15(k + 1) Ta chứng minh: 3(k + 1)3 + 15(k + 1) ⋮ 9
Thật vậy:
3(k + 1)3 + 15(k + 1) = 3. (k3 + 3k2 + 3k + 1) + 15(k + 1)
= 3k3 + 9k2 + 9k + 15k + 18
= 3k3 + 15k + 9(k2 + k + 2)
Vì 3(k + 1)3 + 15(k + 1) (giả thiết quy nạp) và 9(k2 + k + 2) ⋮ 9
Nên: 3(k + 1)3 + 15(k + 1) ⋮ 9
Vậy: 3n3 + 15n chia hết cho 9 với mọi n ∈ N*

có biết đâu mà giúp, mong bạn thông cảm cho. Nhớ tick cho mình với

Phân tích nhân tử nhầm=>giải lại
\(A=2n^2-3n^2+n=n\left(2n^2-3n+1\right)=n\left(n-1\right)\left(2n+1\right)\)\(A=n\left(n-1\right)\left(2n+2-3\right)=\left[2n\left(n-1\right)\left(n+1\right)\right]-3\left(n\right)\left(n-1\right)=2B-3C\)
\(\left\{{}\begin{matrix}B⋮3\\C⋮2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2B⋮6\\3C⋮3\end{matrix}\right.\) \(\Rightarrow A⋮6\) => dpcm
Lời giải:
\(A=n\left(2n^3-3n+1\right)=n\left(n-1\right)\left(2n^2+2n-1\right)\)
\(A=n\left(n-1\right)\left[2n\left(n+1\right)-1\right]=2n\left(n-1\right)\left(n+1\right)+n\left(n-1\right)=B-C\)\(\left\{{}\begin{matrix}B⋮2\\B⋮3\end{matrix}\right.\)\(\Rightarrow B⋮6\forall n\in N\)
\(C=n\left(n-1\right)\) không thể chia hết cho 6 với mọi n thuộc N
\(\Rightarrow A\) chỉ chia hết cho 6 với điều kiện \(n\ne3k+2\)
ví dụ đơn giải với k=0 => n= 2
\(A=2.2^3-3.2^2+2=14⋮̸6\)
Kết luận đề sai

1: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;4;2;-2;-1;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;3;-3\right\}\)
hay \(n\in\left\{0;1;-1\right\}\)

Bài 5:
b: Ta có: \(n+6⋮n+2\)
\(\Leftrightarrow n+2\in\left\{2;4\right\}\)
hay \(n\in\left\{0;2\right\}\)
c: Ta có: \(3n+1⋮n-2\)
\(\Leftrightarrow n-2\in\left\{-1;1;7\right\}\)
hay \(n\in\left\{1;3;9\right\}\)

a, n^3 +5n
= n^3 -n+ 6n
= n(n^2-1)+ 6n
=n(n-1)(n+1) +6n
Vì n(n-1)(n+1) là tích 3 số nguyên liên tiếp nên n(n-1)(n+1) chia hết cho 6
Mặt khác, 6n chia hết cho 6.
Suy ra: n(n-1)(n+1) +6n chia hết cho 6
Vậy n^3 + 5n chia hết cho 6
b, n^3 *19n ko chia hết cho 6 được.Bạn nên xem lại đề bài xem có đúng ko.
c, 5n^3 + 15n^2 +10n
= 5n(n^2 +3n+2)
= 5n(n+1)(n+2)
n(n+1)(n+2) chia hết cho 6 nên 5n^3 +15n^2 +10n chia hết cho 6
Chúc bạn học tốt.
a) Đặt Sn = n3 + 3n2 + 5n
Với n = 1 thì S1 = 9 chia hết cho 3
Giả sử với n = k ≥ 1, ta có Sk = (k3 + 3k2 + 5k)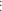 3
3
Ta phải chứng minh rằng Sk+1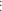 3
3
Thật vậy Sk+1 = (k + 1)3 + 3(k + 1)2 + 5(k + 1)
= k3 + 3k2 + 3k + 1 + 3k2 + 6k + 3 + 5k + 5
= k3 + 3k2 + 5k + 3k2 + 9k + 9
hay Sk+1 = Sk + 3(k2 + 3k + 3)
Theo giả thiết quy nạp thì Sk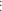 3, mặt khác 3(k2 + 3k + 3)
3, mặt khác 3(k2 + 3k + 3) 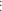 3 nên Sk+1
3 nên Sk+1 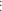 3.
3.
Vậy (n3 + 3n2 + 5n)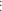 3 với mọi n ε N* .
3 với mọi n ε N* .
b) Đặt Sn = 4n + 15n - 1
Với n = 1, S1 = 41 + 15.1 – 1 = 18 nên S1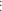 9
9
Giả sử với n = k ≥ 1 thì Sk= 4k + 15k - 1 chia hết cho 9.
Ta phải chứng minh Sk+1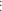 9.
9.
Thật vậy, ta có: Sk+1 = 4k + 1 + 15(k + 1) – 1
= 4(4k + 15k – 1) – 45k + 18 = 4Sk – 9(5k – 2)
Theo giả thiết quy nạp thì Sk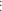 9 nên 4S1
9 nên 4S1 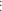 9, mặt khác 9(5k - 2)
9, mặt khác 9(5k - 2) 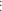 9, nên Sk+1
9, nên Sk+1 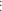 9
9
Vậy (4n + 15n - 1) 9 với mọi n ε N*
9 với mọi n ε N*
c) Đặt Sn = n3 + 11n
Với n = 1, ta có S1 = 13 + 11n = 12 nên S1 6
6
Giả sử với n = k ≥ 1 ,ta có Sk = k3 + 11k 6
6
Ta phải chứng minh Sk+1 6
6
Thật vậy, ta có Sk+1 = (k + 1)3 + 11(k + 1) = k3 + 3k + 3k + 1 + 11k + 11
= ( k3 + 11k) + 3(k2 + k + 4) = Sk + 3(k2 + k + 4)
THeo giả thiết quy nạp thì Sk 6, mặt khác k2 + k + 4 = k(k + 1) + 1 là số chẵn nên 3(k2 + k + 4)
6, mặt khác k2 + k + 4 = k(k + 1) + 1 là số chẵn nên 3(k2 + k + 4)  6, do đó Sk+1
6, do đó Sk+1  6
6
Vậy n3 + 11n chia hết cho 6 với mọi n ε N* .