a) Phát biểu định nghĩa tích phân của hàm số \(f\left(x\right)\) trên một đoạn
b) Nêu các tính chất của tích phân. Cho ví dụ minh họa
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho hàm số y = f(x) liên tục trên [a; b].
F(x) là một nguyên hàm của f(x) trên [a; b].
Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x)
Kí hiệu là 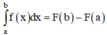

- Tính chất cơ học: Tính cứng, tính dẻo, tính bền,…
- Tính chất vật lí: Nhiệt độ nóng chảy, tính dẫn điện, dẫn nhiệt, khối lượng riêng,…
- Tính chất hoá học: Tính chịu axít, muối, tính chống ăn mòn,…
- Tính chất công nghệ: Tính đúc, tính hàn, tính rèn, khả năng gia công cắt gọt,…

a, Tìm giá trị phân số của một số cho trước
- Quy tắc: Muốn tìm \(\dfrac{m}{n}\) của b cho trước, ta tính b.\(\dfrac{m}{n}\)
VD: 0,25 của 1 giờ
Đổi 1 giờ= 60 phút
60.0,25=15 phút
b, Tìm một số biết giá trị phân số của nó:
- Quy tắc: Muốn tìm một số biết \(\dfrac{m}{n}\) của số đó, ta lấy a:\(\dfrac{m}{n}\)
VD: \(\dfrac{2}{3}\) của nó bằng 7,2: \(\dfrac{2}{3}=10,8\)
c, Tìm tỉ số của a và b
- Quy tắc: Thương trong phép chia a cho b (b≠0) là tỉ số của a và b
VD: Tỉ số giữa a và b là a:b hoặc \(\dfrac{a}{b}\)

Câu 1:
+ Tác dụng với kim loại: O2 oxi hóa được hầu hết các kim loại trừ Ag, Au, Pt
+ Tác dụng với Hiđro, Phản ứng có thể gây nổ mạnh nếu tỉ lệ phản ứng O2:H2 = 1:2
+ Tác dụng với một số phi kim khác:
+ Tác dụng với một số hợp chất:
Câu 2:
+ Phản ứng hóa hợp là PƯHH trong đó có một chất mới được tạo thành từ hai hay nhiều chất ban đầu.
+ Phản ứng phân hủy là PƯHH trong đó có 2 hay nhiều chất được tạo thành từ một chất ban đầu.
Câu 2:
+ Phản ứng hóa hợp là PƯHH trong đó có một chất mới được tạo thành từ hai hay nhiều chất ban đầu.
+ Phản ứng phân hủy là PƯHH trong đó có 2 hay nhiều chất được tạo thành từ một chất ban đầu.

5.Phân số tối giản là phân số không thể rút gọn được nữa. VD : 4/5
4. muốn rút gọn phân số ta lấy cả tử vs mẫu chia cho 1 số nào đó
VD: \(\frac{10}{15}=\frac{10:5}{15:5}=\frac{2}{3}\)
Lời giải:
Cho hàm số y= f(x) liên tục trên [a; b] , F(x) là một nguyên hàm của f(x) trên [a; b]. Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là ∫abf(x)dx.
Ta có: ∫abf(x)dx=F(x)ab=F(b)-F(a)
Ta gọi ∫ab là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx biểu thức dưới dấu tích phân, f(x) là hàm số dưới dấu tích phân.
2.Các tính chất
1. ∫aaf(x)dx=0
2. ∫abf(x)dx=- ∫baf(x)dx
3. ∫bakf(x)dx=k. ∫baf(x)dx ( k là hằng số)
4. ∫ab[f(x)±g(x)]dx= ∫abf(x)dx± ∫abg(x)dx
5. ∫abf(x)dx= ∫acf(x)dx+ ∫abf(x)dx(a<c<b)