Tìm nguyên hàm của các hàm số sau :
a) \(f\left(x\right)=\dfrac{x+\sqrt{x}+1}{\sqrt[3]{x}}\)
b) \(f\left(x\right)=\dfrac{2^x-1}{e^x}\)
c) \(f\left(x\right)=\dfrac{1}{\sin^2x.\cos^2x}\)
d) \(f\left(x\right)=\sin5x.\cos3x\)
e) \(f\left(x\right)=\tan^2x\)
g) \(f\left(x\right)=e^{3-2x}\)
h) \(f\left(x\right)=\dfrac{1}{\left(1+x\right)\left(1-2x\right)}\)

a) Điều kiện x>0. Thực hiện chia tử cho mẫu ta được:
f(x) =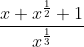 =
= 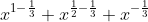 =
= 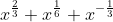
∫f(x)dx = ∫(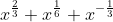 )dx =
)dx = 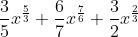 +C
+C
b) Ta có f(x) =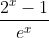 =
= 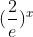 -e-x
-e-x
; do đó nguyên hàm của f(x) là:
F(x)=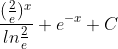 =
=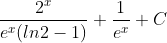 =
= 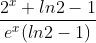 + C
+ C
c) Ta có f(x) =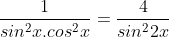
hoặc f(x) =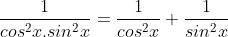
Do đó nguyên hàm của f(x) là F(x)= -2cot2x + C
d) Áp dụng công thức biến tích thành tổng:
f(x) =sin5xcos3x = (sin8x +sin2x).
(sin8x +sin2x).
Vậy nguyên hàm của hàm số f(x) là F(x) = - (
( cos8x + cos2x) +C
cos8x + cos2x) +C
e) ta có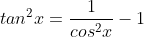
vậy nguyên hàm của hàm số f(x) là F(x) = tanx - x + C
g) Ta có ∫e3-2xdx= - ∫e3-2xd(3-2x)= -
∫e3-2xd(3-2x)= - e3-2x +C
e3-2x +C
h) Ta có :
=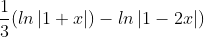 =
= 