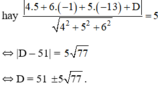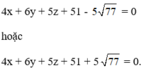Viết phương trình mặt phẳng \(\left(\alpha\right)\) tiếp xúc với mặt cầu :
\(\left(S\right):x^2+y^2+z^2-10x+2y+26z+170=0\)
và song song với hai đường thẳng :
\(d:\left\{{}\begin{matrix}x=-5+2t\\y=1-3t\\z=-13+2t\end{matrix}\right.\) và \(d':\left\{{}\begin{matrix}x=-7+3t'\\y=-1-2t'\\z=8\end{matrix}\right.\)


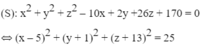
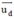 = (2; -3; 2) và
= (2; -3; 2) và 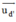 = (3 ; -2 ; 0) là các vtcp
= (3 ; -2 ; 0) là các vtcp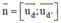 = (4; 6; 5) là vtpt
= (4; 6; 5) là vtpt