Cho một điểm A cố định và một đường thẳng a cố định không đi qua A. Gọi O là một điểm thay đổi trên a. Chứng minh rằng các mặt cầu tâm O bán kính r = OA luôn luôn đi qua một đường tròn cố định ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 7 2018
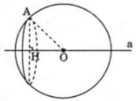
Gọi (P) là mặt phẳng đi qua A và vuông góc với đường thẳng a tại H. Khi đó (P) và H cố định.
Ta có: (P) cắt mặt cầu S(O; R) theo đường tròn tâm H và bán kính HA không đổi.
Vậy các mặt cầu tâm O bán kính R = OA luôn đi qua đường tròn cố định tâm H bán kính bằng HA.
6 tháng 2 2021
Ta có PQI = PIA ( cùng chắn PI) nên ΔAPI ~ΔAIQ(g.g）
=> AP/AI = AI/AQ =>Ap.AQ= AI^2 ( không đổi )
Giả sử đt ngoại tiếp tấm giác BPQ cắt AB tại D (D khác B)
Khi đó tam giác ADP ~ tam giác AQB =>AD/AQ = AP/AB
hay AD.AB = AP.AQ=AI^2 ( không đổi)
Do đó điểm D là điểm cố định (đpcm)
CM
22 tháng 7 2019
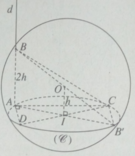
Tam giác ADC vuông tại A nên AD 2 = DC 2 - AC 2 (1)
Tam giác ABC vuông tại A nên BC 2 = AC 2 + AB 2 (2)
Từ (1) và (2) ta suy ra AD 2 + BC 2 = DC 2 + AB 2 (3)
Ta lại có:
AC 2 = DC 2 - AD 2 và BD 2 = AD 2 + AB 2 (4)
DC 2 = 4 r 2 - h 2 , AB 2 = 4 h 2 (5)
Từ (4) và (5) ta có:
AC 2 + BD 2 = DC 2 + AB 2 = 4 r 2 - h 2 + 4 h 2 = 4 r 2 (6)
Từ (3) và (6) ta có: AD 2 + BC 2 = AC 2 + BD 2 (không đổi)
2 tháng 8 2017
Gọi I là giao điểm của MN và AC.
Ta có: \(\widehat{IHO}=\widehat{OEI}=90°\)
\(\Rightarrow\)Tứ giác EIHO nội tiếp đường tròn.
\(\Rightarrow\)Tâm của đường tròn ngoại tiếp ∆OHE nằm trên đường trung trực của EI.(*)
Ta có ∆AIH \(\approx\)∆AOE
\(\Rightarrow\)AH.AO = AE.AI (1)
Ta có: ∆AMB \(\approx\)AOM
\(\Rightarrow\)AM2 = AH.AO (2)
Ta lại có: ∆ABM \(\approx\)∆AMC
\(\Rightarrow\)AM2 = AB.AC (3)
Từ (1), (2), (3) \(\Rightarrow\)AE.AI = AB.AC
Vì A,B,C,E cố định nên I cố định (**)
Từ (*), (**) suy ta tâm đường tròn ngoại tiếp ∆OHE nằm trên đường trung trực của EI.
PS: không chứng minh được nó nằm trên đường tròn nha b. Hình tự vẽ.
Xét mặt phẳng (P) qua điểm A và (P) vuông góc với đường thẳng a. GỌi giao của (P) với a là điểm I. Xét mặt cầu tâm O bán kính r = OA; mặt cầu này giao với mặt phẳng (P) theo đường tròn tâm I là hình chiếu vuông góc của O lên (P) và bán kính IA = r2 cố định