Thế nào là hai hình bằng nhau, hai hình đồng dạng với nhau ?
Cho ví dụ ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
5 tháng 7 2019
+ Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
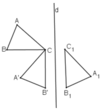
Ví dụ: ΔABC sau khi thực hiện phép quay tâm C, góc 90º rồi lấy đối xứng qua d được ΔA1B1C1.
⇒ ΔABC = ΔA1B1C1
+ Hai hình được gọi là đồng dạng nếu có một phép đồng dạng biến hình này thành hình kia.
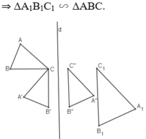
Ví dụ: ΔABC sau khi thực hiện liên tiếp phép quay tâm C góc 90º; đối xứng qua đường thẳng d và phép vị tự tâm B tỉ số 1,5 được ΔA1B1C1
NY
0
PT
1
CM
6 tháng 7 2017
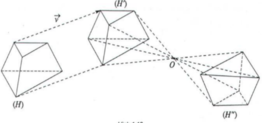
- Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến đa diện này thành đa diện kia.
- Ví dụ về đa diện bằng nhau:
CM
11 tháng 12 2017
Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.
Ví dụ: –2x2y ; 3x2y ; 5x2y là các đơn thức đồng dạng, ta có thể cộng (hay trừ) các hệ số với nhau và giữ nguyên phần biến.
27 tháng 4 2016
Hai phân số : \(\frac{a}{b}\) và \(\frac{c}{d}\) gọi là bằng nhau nếu a . d = b.c
Có 4 trường hợp
\(\frac{a}{b}=\frac{c}{d};\frac{a}{c}=\frac{b}{d};\frac{d}{b}=\frac{c}{a};\frac{d}{c}=\frac{b}{a}\)
Ví dụ :
1 ) \(-\frac{3}{4}=\frac{6}{-8}vì\left(-3\right).\left(-8\right)=4.6\)
27 tháng 4 2016
Phân số bằng nhau là khi ta quy đồng cả tử cả mẫu cùng một số . Ví dụ : 2/3=4/6
Định nghĩa:
Hai hình gọi là bằng nhau nếu có phép dời hình biến hình này thành hình kia.
Ví dụ:
Cho hình bình hành ABCD, khi đó một đường thẳng bất kỳ đi qua tâm O của ABCD, luôn chia hình bình hành ABCD ra thành hai hình bằng nhau.
Định nghĩa:
Hai hình gọi là bằng nhau nếu có phép dời hình biến hình này thành hình kia.
Ví dụ:
Cho hình bình hành ABCD, khi đó một đường thẳng bất kỳ đi qua tâm O của ABCD, luôn chia hình bình hành ABCD ra thành hai hình bằng nhau.