Chứng minh rằng khi thực hiện liên tiếp hai phép vị tự tâm O sẽ được một phép vị tự tâm O ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 12 2018
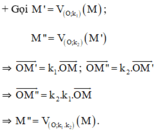
Vậy khi thực hiện liên tiếp hai phép vị tự tâm O với tỉ số k1 và k2 thì ta được 1 phép vị tự tâm O với tỉ số k1.k2.
CM
15 tháng 5 2018
Đáp án D
(C) có tâm O(2;–6), bán kính 2
I ' = V O ; k ( I ) -> − 1 2 O I → = O I ' → -> O’(–1;3), bán kính
Q ( O ; 90 o ) : I ' → I " − 3 ; − 1 , bán kính 1
Phương trình đường tròn (C”): x + 3 2 + y + 1 2 = 1
CM
5 tháng 10 2019
Đáp án A
M ' = V O ; k ( M ) => M’(12;12)
T u → ( M ' ) = M ' ' => M”(10;9)
CM
3 tháng 1 2017
+ Gọi (I1; R1) = Q(O; 45º) (I; R) (Phép quay đường tròn tâm I, bán kính R qua tâm O một góc 45º).
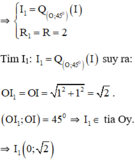
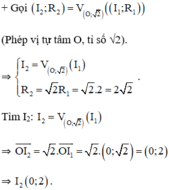
Vậy phương trình đường tròn cần tìm là (I2; R2): x2 + (y – 2)2 = 8.
CM
15 tháng 8 2017
Đáp án C
Những phát biểuđúng: 1; 4; 5; 6; 7; 8; 9; 10; 11; 13; 14
2. Qua phép vị tự có tỉ số , đường tròn có tâm là tâm vị tự sẽ biến thành 1 đường tròn đồng tâm với đường tròn ban đầu và có bán kính = k. bán kính đường tròn ban đầu.
3. Qua phép vị tự có tỉ số đường tròn biến thành chính nó.
12. Phép vị tự với tỉ số k = biến tứ giác thành tứ giác bằng nó
CM
16 tháng 12 2019
Đáp án D
Q ( O ; 180 o ) : I → I ' (0;1) , bán kính 2
I ' ' = V O ; k ( I ' ) -> I”(0;2), bán kính 4
Phương trình đường tròn (C”): x 2 + y − 2 2 = 16
CM
22 tháng 11 2018
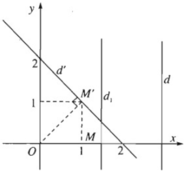
Gọi d 1 là ảnh của d qua phép vị tự tâm O tỉ số k = 0,5 thì phương trình của d 1 là x = 2 . Giả sử d' là ảnh của d qua phép quay tâm O góc 45 ο . Lấy M ( 2 ; 0 ) thuộc d 1 thì ảnh của nó qua phép quay tâm O góc 45 ο là M′(1;1) thuộc d'. Vì OM ⊥ d 1 nên OM′ ⊥ d′. Vậy d' là đường thẳng đi qua M' và vuông góc với OM'. Do đó nó có phương trình x + y – 2 = 0.
Với mỗi điểm M, gọi M' =%7D%7D%5E%7B%7D)
(M), M''=%7D%7D%5E%7B%7D)
(M').
Khi đó:
= k 
, 
= p 
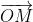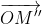= pk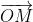 
.
Từ đó suy ra M''=%7D%7D%5E%7B%7D)
(M). Vậy thực hiện liên tiếp hai phép vị tự %7D%7D%5E%7B%7D)
và %7D%7D%5E%7B%7D)
sẽ được phép vị tự %7D%7D%5E%7B%7D)
Với mỗi điểm M, gọi M' =%7D%7D%5E%7B%7D)
(M), M''=%7D%7D%5E%7B%7D)
(M'). Khi đó: 
= k 
, 
= p 
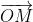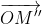= pk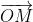 
. Từ đó suy ra M''= %7D%7D%5E%7B%7D)
(M). Vậy thực hiện liên tiếp hai phép vị tự %7D%7D%5E%7B%7D)
và %7D%7D%5E%7B%7D)
sẽ được phép vị tự %7D%7D%5E%7B%7D)
.