Question

[Sách Giáo Khoa]

Lập phương trình đường tròn (C) trong các trường hợp sau :

a) (C) có tâm \(I\left(-2;3\right)\) và đi qua \(M\left(2;-3\right)\)

b) (C) có tâm \(I\left(-1;2\right)\) và tiếp xúc với đường thẳng \(x-2y+7=0\)

c) (C) có đường kính AB với \(A=\left(1;1\right)\) và \(B=\left(7;5\right)\)

Answer 1

[Đức Minh]

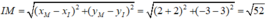
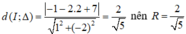
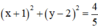
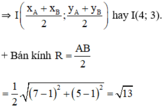
a) Ta tìm bán kính R² = IM² => R² = IM = (2 + 2)² + (-3 -3²) = 52

Phương trình đường tròn (C): (x +2)² + (y – 3)² =52

b) Đường tròn tiếp xúc với đường thẳng d nên khoảng cách từ tâm I tới đường thẳng d phải bằng bán kính đường tròn:

d(I; d) = R

Ta có : R = d(I; d) = \(=\)

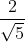
Phương trình đường tròn cần tìm là:

(x +1)² + (y – 2)² =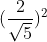 =>( x +1)² + (y – 2)² =

<=> 5x² + 5y² +10x – 20y +21 = 0

c) Tâm I là trung điểm của AB, có tọa độ :

x = \(\dfrac{1+7}{2}\) = 4; y = \(\dfrac{1+5}{2}\) = 3 => I(4; 3)

AB = \(2\sqrt{13}\) => R =\(\sqrt{13}\)

=> (x -4 )² + (y – 3)² =13