Khi nào hai phương trình được gọi là tương đương ? Cho ví dụ ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Hai phương trình có cùng tập nghiệm thì tương đương nhau.
- Ví dụ hai phương trình:
x2 - 3x + 2 = 0 và (x - 1)(x - 2)(x2 + x + 1) = 0
là hai phương trình tương đương vì chúng có cùng tập nghiệm là {1, 2}.

Ví dụ: phương trình (1) x - 1 = 3 có tập nghiệm S1 = {4}.
Nhân hai vế của phương trình (1) với x, ta được phương trình:
(x - 1)x = 3x (2)
⇔ (x - 1)x - 3x = 0
⇔ x(x - 4) = 0
Phương trình (2) có tập nghiệm là S2 = {0, 4}.
Vì S1 ≠ S2 nên hai phương trình (1) và (2) không tương đương.

Ví dụ: phương trình (1) x - 1 = 3 có tập nghiệm S1 = {4}.
Nhân hai vế của phương trình (1) với x, ta được phương trình:
(x - 1)x = 3x (2)
⇔ (x - 1)x - 3x = 0
⇔ x(x - 4) = 0
Phương trình (2) có tập nghiệm là S2 = {0, 4}.
Vì S1 ≠ S2 nên hai phương trình (1) và (2) không tương đương.
3. Với điều kiện nào của a thì phương trình ax + b = 0 là một phương trình bậc nhất? (a và b là hai hằng số).

uses crt;
var i,n,m,k,d:integer;
{---------------chuong-trinh-con-tim-ucln--------------------}
function ucln(x,y:integer):integer;
var t:integer;
begin
while y<>0 do
begin
t:=x mod y;
x:=y;
y:=t;
end;
ucln:=x;
end;
{------------chuong-trinh-con-kiem-tra-so-nguyen-to-------------------}
function nt(b:longint):boolean;
var j:longint;
begin
nt:=true;
if (b=2) or (b=3) then exit;
nt:=false;
if (b=1) or (b mod 2=0) or (b mod 3=0) then exit;
j:=5;
while j<=trunc(sqrt(b)) do
begin
if (b mod j=0) or (b mod (j+2)=0) then exit;
j:=j+6;
end;
nt:=true;
end;
{---------------chuong-trinh-chinh---------------------}
begin
clrscr;
write('Nhap N: '); readln(N);
write('Nhap M: '); readln(M);
d:=0;
k:=ucln(N,M);
for i:=1 to k do
if nt(i) then d:=d+1;
if d>0 then writeln('2 so nay tuong duong voi nhau')
else writeln('2 so nay khong tuong duong voi nhau');
readln;
end.

Hai phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.
Đáp án cần chọn là: C

Hai bất phương trình trong VD 1 không tương đương do chúng không có cùng tập nghiệm.


- Bạn Nga đã nhận xét đúng vì hai hệ phương trình cùng vô nghiệm có nghĩa là chúng cùng có tập nghiệm bằng ∅.
- Bạn Phương nhận xét sai.
Ví dụ: Xét hai hệ 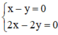 và
và 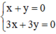
Hệ 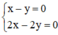 có vô số nghiệm. Tập nghiệm của (I) được biểu diễn bởi đường thẳng x – y = 0.
có vô số nghiệm. Tập nghiệm của (I) được biểu diễn bởi đường thẳng x – y = 0.
Hệ 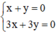 có vô số nghiệm. Tập nghiệm của (II) được biểu diễn bởi đường thẳng x + y = 0.
có vô số nghiệm. Tập nghiệm của (II) được biểu diễn bởi đường thẳng x + y = 0.
Nhận thấy, tập nghiệm của hai hệ (I) và hệ (II) được biểu diễn bởi hai đường thẳng khác nhau nên hai hệ không tương đương.
Hai phương trình (cùng ẩn) được gọi là tương đương nếu chúng có cùng tập nghiệm.
Hai phương trình \(2x-5=0\)và \(3x-\dfrac{15}{2}=0\) tương đương với nhau vì cùng có nghiệm duy nhất \(x=\dfrac{5}{2}\)
Hai phương trình (cùng ẩn) được gọi là tương đương nếu chúng có cùng tập nghiệm.
Nếu f(x) = g(x) tương đương với f1(x) = g1(x) thì ta viết:
f(x) = g(x) f1(x) = g1(x)
f1(x) = g1(x)
Ví dụ: