Biết x, y là các số nguyên:
Giá trị nhỏ nhất của A =(2x-1)^2014+(3y-4)^2016 là bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
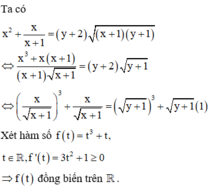
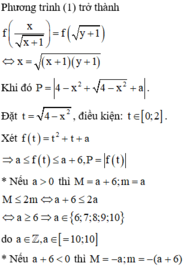
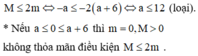
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.

a) Có: \(\hept{\begin{cases}\left(2x-1\right)^{2014}\ge0\forall x\\\left|2x-y+4\right|\ge0\forall x;y\end{cases}}\)
\(\Rightarrow\left(2x-1\right)^{2014}+\left|2x-y+4\right|\ge0\forall x;y\)
\(\Rightarrow P\ge-2016\)
Dấu "=" xảy ra khi: \(\hept{\begin{cases}\left(2x-1\right)^{2014}=0\\\left|2x-y+4\right|=0\end{cases}\Rightarrow\hept{\begin{cases}2x-1=0\\2x-y+4=0\end{cases}\Rightarrow}\hept{\begin{cases}x=\frac{1}{2}\\2x-y=-4\end{cases}\Rightarrow}y=5}\)
vậy minP=-2016 khi x=1/2; y=5
b) có:\(\left|x-8\right|+\left|x+3\right|=\left|8-x\right|+\left|x+3\right|\ge\left|8-x+x+3\right|=\left|11\right|=11\)
\(\Rightarrow Q\ge11-15=-4\)
dấu "=" xảy ra khi: (x-8)(x+3)>=0
Suy ra: 8 >= x >= -3
vậy minQ=-4 khi 8 >= x >= -3
Các số mũ của nó đều mũ chẵn nên lũy thừa sẽ dương với mọi x, y.
Suy ra cả tổng lớn hơn hoặc bằng 0. Vậy GTNN của tổng là 0 khi cả hai lũy thừa bằng 0. Cả 2 lũy thừa bằng 0 khi và chỉ khi... tự tính tiếp.