Sử dụng hằng đẳng thức khai triển và thu gọn biểu thức sau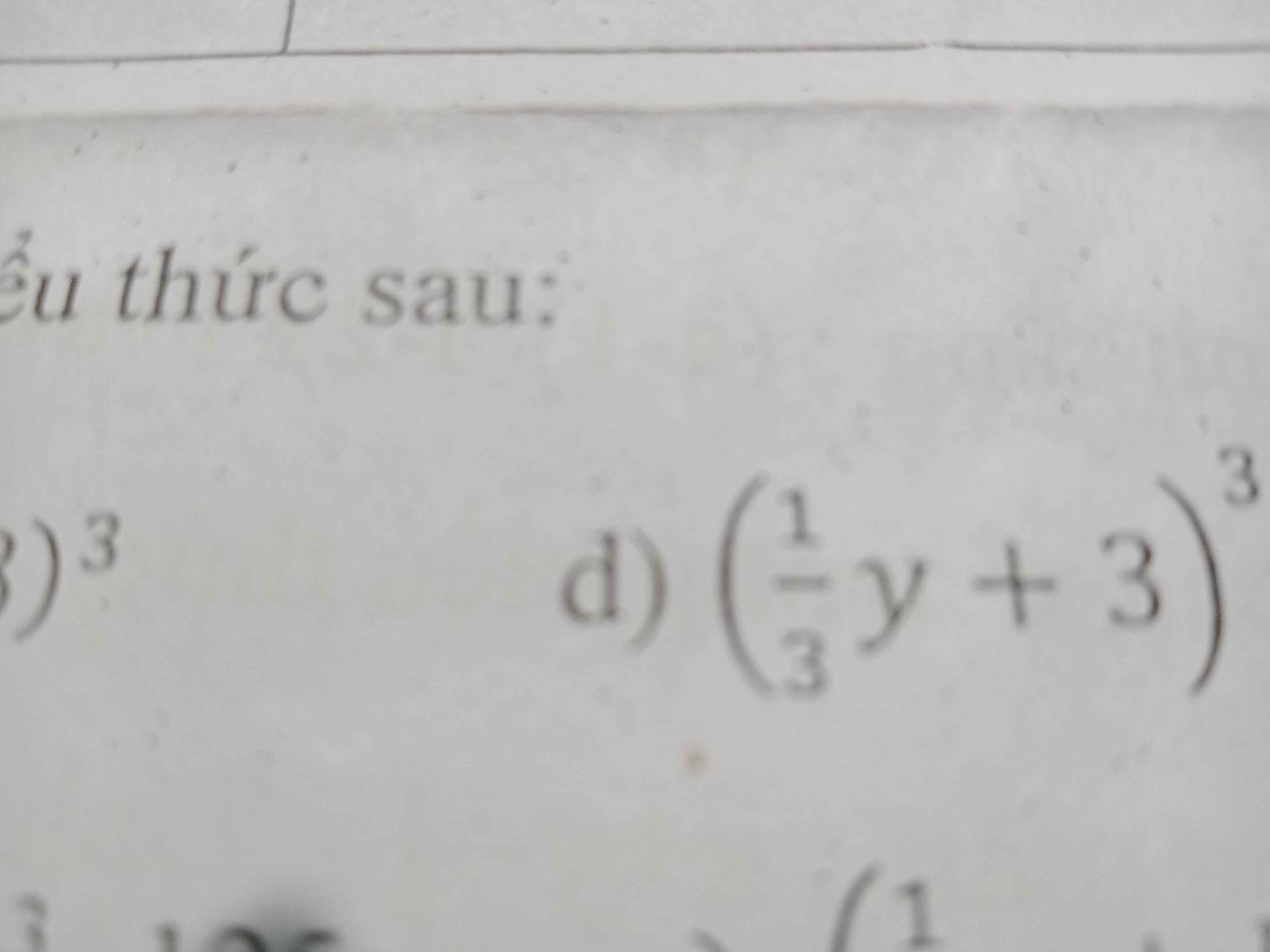
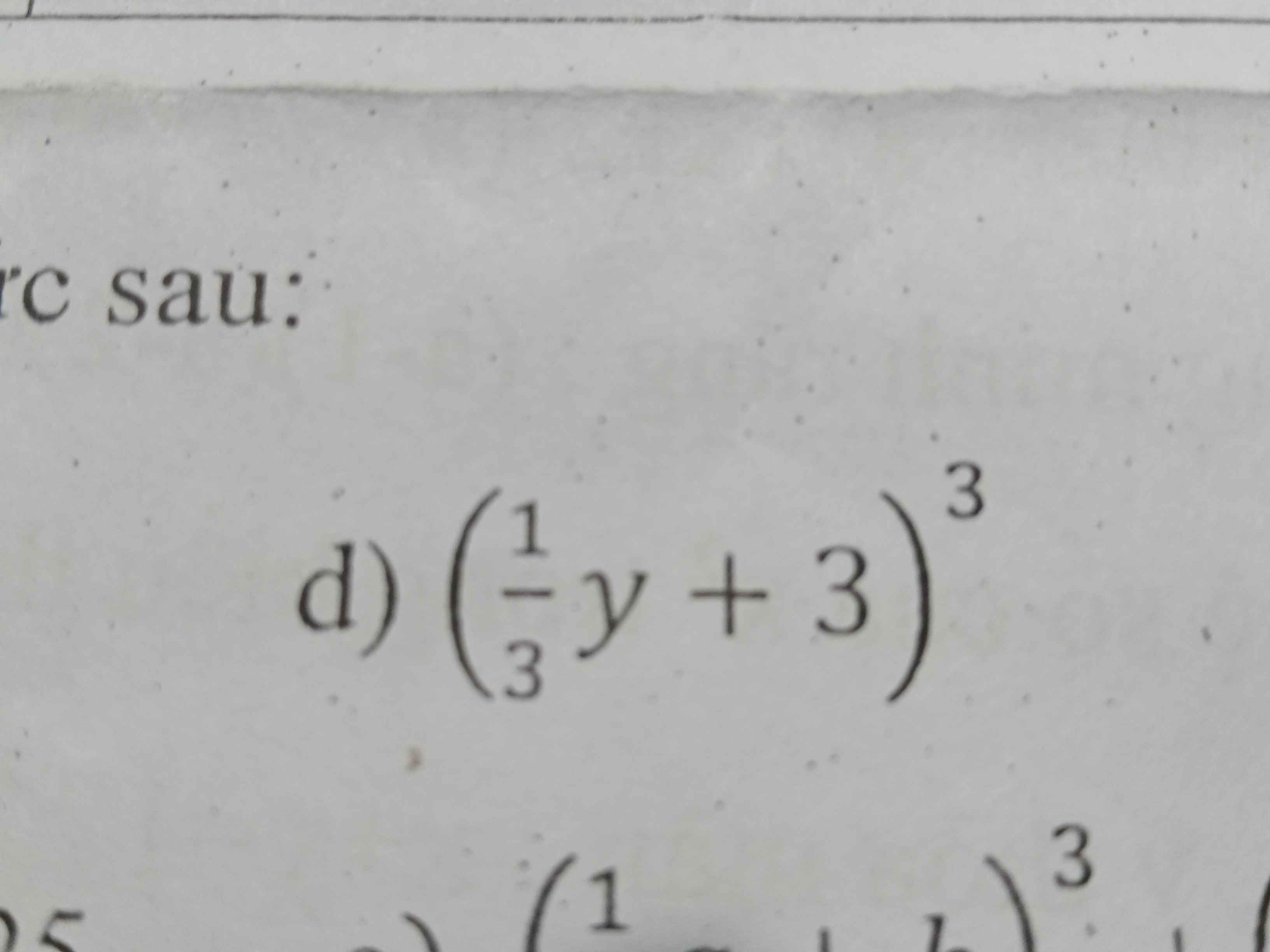
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(\dfrac{1}{3y+3}\right)^3=\dfrac{1}{\left(3y+3\right)^3}=\dfrac{1}{27y^3+81y^2+81y+27}\)
\(\left(\dfrac{1}{3y+3}\right)^3=\dfrac{1^3}{\left(3y+3\right)^3}=\dfrac{1}{27\left(y^3+3y^2+3y+1\right)}\)

a: Ta có: \(\left(x+y\right)^3-\left(x-y\right)^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)
\(=6x^2y+2y^3\)

\(\left(x+y\right)^3=x^3+3x^2y+3xy^2-y^3\)
\(\left(x-y\right)^3=x^3-3x^2y+3xy^2-y^3\)
\(\left(2y-3\right)^3=8y^3-36y^2+54y-27\)
a: Ta có: \(\left(x+y\right)^3-\left(x-y\right)^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)
\(=6x^2y+2y^3\)

Ta có:(a2+ab+b2)(a2-ab+b2)-(a4+b4)
= (a2+b2)2-a2b2-a4-b4=a4+2a2b2+b4-a2b2-a4-b4=a2b2
Ta có:(a2+ab+b2)(a2-ab+b2)-(a4+b4)
= (a2+b2)2-a2b2-a4-b4=a4+2a2b2+b4-a2b2-a4-b4=a2b2

Lời giải:
\(A=(x+2y+3z)(x-2y+3z)\)
\(=[(x+3z)+2y][(x+3z)-2y]\)
\(=(x+3z)^2-(2y)^2\)
\(=x^2+9z^2+6xz-4y^2\)
(1𝑦/3+3)^3
(𝑦/3+3)^3
(𝑦/3+3⋅3/3)^3
(𝑦+3⋅3/3)^3
(𝑦+9/3)^3
\(\left(\dfrac{1}{3}y+3\right)^3=\dfrac{1}{27}y^3+y^2+9y+27\)