Cho mạch điện như hình vẽ: Hiệu điện thế giữa hai điểm B, D không đổi khi mở và đóng khoá K, vôn kế lần lượt chỉ hai giá trị U1 và U2. Biết rằng R2 = 4R1 và vôn kế có điện trở rất lớn. Tính hiệu điện thế giữa hai đầu B, D theo U1 và U2.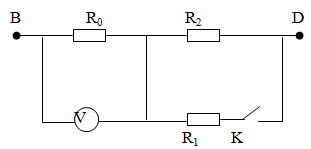
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi khoá K mở, trong mạch không có dòng điện. Ta có: U V = E = 6 V
Khi đóng K, trong mạch có dòng điện: I = E R 1 + R 2 + r = 6 11 , 5 + r
Số chỉ vôn kế V chính là hiệu điện thế hai cực của nguồn nên:
U ' V = E ' − I . r ⇔ 5 , 75 = 6 − 6 11 , 5 + r . r ⇒ r = 0 , 5 Ω ⇒ I = 0 , 5 A
Số chỉ của ampe kế A chính là dòng điện trong mạch chính nên I A = I = 0 , 5 A
Chọn A

a) Ban đầu khóa K mở, R 4 = 4 Ω , vôn kế chỉ 1 V.
Xác định hiệu điện thế U:
Ta có:
R 12 = R 1 + R 2 = 6 Ω ; R 34 = R 3 + R 4 = 6 Ω ; I 12 = I 1 = I 2 = U R 12 = U 6 I 34 = I 3 = I 4 = U R 34 = U 6 ;
U M N = V M - V N = V A - V N - V A + V M = I 3 . R 3 - I 1 . R 1 = U 6 . 2 - U 6 . 3 = - U 6 ⇒ U V = U N M = U 6 = 1 V ⇒ U = 6 V
Khi khóa K đóng:
R 13 = R 1 R 3 R 1 + R 3 = 3 . 2 3 + 2 = 6 5 = 1 , 2 ( Ω ) ; R 24 = R 2 R 4 R 2 + R 4 = 3 . 4 3 + 4 = 12 7 ( Ω ) R B D = R 13 + R 24 = 1 , 2 + 12 7 = 20 , 4 7 ( Ω )
Cường độ dòng điện mạch chính:
I = U R B D = 6 20 , 4 7 = 42 20 , 4 = 21 10 , 2 ≈ 2 , 06 ( A ) ; U 13 = U 1 = U 3 = I . R 13 = 21 10 , 2 . 1 , 2 = 2 , 47 ( V ) ; I 1 = U 1 R 1 = 2 , 47 3 = 0 , 823 ( A ) ; U 24 = U 2 = U 4 = I . R 24 = 21 10 , 2 . 12 7 = 3 , 53 ( V ) I 2 = U 2 R 2 = 3 , 53 3 = 1 , 18 ( A )
Ta có : I 2 > I 1 ⇒ I A = I 2 - I 1 = 1 , 18 - 0 , 823 = 0 , 357 ( A ) . Vậy dòng điện qua ampe kế có chiều từ N đến M và có cường độ I A = 0 , 357 ( A ) ; vôn kế chỉ 0 (V)
b) Đóng khóa K và di chuyển con chạy C của biến trở R4 từ đầu bên trái sang đầu bên phải thì số chỉ của ampe kế I A thay đổi như thế nào?
Ta có: R 13 = R 1 R 3 R 1 + R 3 = 3 . 2 3 + 2 = 6 5 = 1 , 2 Ω
Đặt phần điện trở còn hoạt động trong mạch của R 4 là x, ta có:
R 24 = R 2 x R 2 + x = 3 x 3 + x ; R B D = 1 , 2 + 3 x 3 + x = 4 , 2 x + 3 , 6 3 + x ; I = U R B D = 6 4 , 2 x + 3 , 6 3 + x . 1 , 2 = 7 , 2 ( 3 + x ) 4 , 2 x + 3 , 6 ; I 1 = U 13 R 1 = 7 , 2 ( 3 + x ) 4 , 2 x + 3 , 6 3 = 2 , 4 ( 3 + x ) 4 , 2 x + 3 , 6 U 24 = I . R 24 = 6 ( 3 + x ) 4 , 2 x + 3 , 6 . 3 x 3 + x = 18 x 4 , 2 x + 3 . 6 I 2 = U 24 R 2 = 18 x 4 , 2 x + 3 , 6 3 = 6 x 4 , 2 x + 3 , 6
* Xét hai trường hợp:
- Trường hợp 1: Dòng điện chạy qua ampe kế có chiều từ M đến N.
Khi đó : I A = I 1 - I 2 = 2 , 4 ( 3 + x ) 4 , 2 x + 3 , 6 - 6 x 4 , 2 x + 3 , 6 = 7 , 2 - 3 , 6 x 4 , 2 x + 3 , 6 (1)
Biện luận: Khi x = 0 → I A = 2 ( A )
Khi x tăng thì (7,2 - 3,6.x) giảm; (4,2.x + 3,6) tăng do đó I A giảm
Khi x = 2 → I A = 7 , 2 - 3 , 6 . 2 4 , 2 . 2 + 3 , 6 = 0 .
- Trường hợp 2 : Dòng điện chạy qua ampe kế có chiều từ N đến M.
Khi đó : I A = I 2 - I 1 = 6 x 4 , 2 x + 3 , 6 - 2 , 4 ( 3 + x ) 4 , 2 x + 3 , 6 = 3 , 6 x - 7 , 2 4 , 2 x + 3 , 6
I A = 3 , 6 - 7 , 2 x 4 , 2 + 3 , 6 x (2)
Biện luận:
Khi x tăng từ 2 W trở lên thì 7 , 2 x và 3 , 6 x đều giảm do đó IA tăng.
Khi x rất lớn (x = ∞ ) thì 7 , 2 x và 3 , 6 x tiến tới 0. Do đó IA 0,86 (A) và cường độ dòng chạy qua điện trở R 4 rất nhỏ.

Bài này khảo sát \(U_L\) theo \(C\)
+ Khi C = C1 vôn kế chỉ U1, khi C biến thiên U giảm, do đó C = C1 thì cộng hưởng xảy ra.
\(Z_L=Z_{C1}\)
+ Khi C2=2C1 \(\Rightarrow Z_{C2}=\dfrac{Z_{C1}}{2}=\dfrac{Z_L}{2}\)
\(U_2=\dfrac{U_1}{2}\) \(\Rightarrow I_2=\dfrac{I_1}{2}\) (vì ZL không đổi)
\(\Rightarrow Z_2=2Z_1\)
\(\Rightarrow \sqrt{R^2+(\dfrac{Z_L}{2})^2}=2R\)
\(\Rightarrow Z_L=Z_{C1}=2\sqrt 3 R\)
+ Để U3 = U2/2 = U1/4
\(\Rightarrow I_3=I_1/4\)
\(\Rightarrow Z_3=4Z_1\)
\(\Rightarrow \sqrt{R^2+(Z_L-Z_{C3})^2}=4R\)
\(\Rightarrow |Z_L-Z_{C3}|=\sqrt {15} R\)
\(\Rightarrow |Z_{C1}-Z_{C3}|=\sqrt{15}.\dfrac{2}{\sqrt 3}Z_{C1}=2\sqrt 5 Z_{C1}\)
\(\Rightarrow Z_{C3}=(1+2\sqrt 5)Z_{C1}\)
\(\Rightarrow C_3=\dfrac{C_1}{1+2\sqrt5}\)
TH1: K mở =>R0 nt R2
\(=>U1=I0.R0\left(V\right)\)
\(=>Ubd=I0.Rtd=\dfrac{U1}{R0}\left(R0+R2\right)=>Ubd=U1+\dfrac{U1.R2}{R0}\)
\(=>\dfrac{U1.R2}{R0}=Ubd-U1=>R0=\dfrac{U1.R2}{Ubd-U1}\)
Th2: R0 nt (R1//R2)
\(=>U0=U2\)
\(=>Ubd=U2+I0.R12=U2+\dfrac{U2}{R0}.\dfrac{R1.R2}{R1+R2}\)
\(=>Ubd=U2+\dfrac{U2}{R0}.\dfrac{\dfrac{R2}{4}.R2}{\dfrac{R2}{4}+R2}=U2+\dfrac{U2}{R0}.\dfrac{\dfrac{R2^2}{4}}{\dfrac{5R2}{4}}\)
\(=U2+\dfrac{U2}{R0}.\dfrac{R2}{5}=>Ubd=U2+\dfrac{U2.R2}{5R0}\)
\(=>R0=\dfrac{U2.R2}{5\left(Ubd-U2\right)}\)
\(=>\dfrac{U1.R2}{Ubd-U1}=\dfrac{U2.R2}{5\left(Ubd-U2\right)}\)
\(=>Ubd=\dfrac{4U1U2}{5U1-U2}\)