Tính tổng : \(\dfrac{1}{5}+\dfrac{1}{20}+\dfrac{1}{44}+\dfrac{1}{77}+\dfrac{1}{119}+\dfrac{1}{170}+\dfrac{1}{230}+\dfrac{1}{299}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu C giải rồi
\(B=\dfrac{1}{5}+\dfrac{1}{20}+\dfrac{1}{44}+\dfrac{1}{77}+\dfrac{1}{119}+\dfrac{1}{170}+\dfrac{1}{230}+\dfrac{1}{299}\)
\(=2\left(\dfrac{1}{10}+\dfrac{1}{40}+\dfrac{1}{88}+\dfrac{1}{154}+\dfrac{1}{238}+\dfrac{1}{340}+\dfrac{1}{460}+\dfrac{1}{598}\right)\)
\(=\dfrac{2}{3}\left(\dfrac{3}{2.5}+\dfrac{3}{5.8}+\dfrac{3}{8.11}+\dfrac{3}{11.14}+\dfrac{3}{14.17}+\dfrac{3}{17.20}+\dfrac{3}{20.23}+\dfrac{3}{23.26}\right)\)
\(=\dfrac{2}{3}\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+...+\dfrac{1}{23}-\dfrac{1}{26}\right)\)
\(=\dfrac{2}{3}\left(\dfrac{1}{2}-\dfrac{1}{26}\right)=\dfrac{4}{13}\)

ta tách 2/5x7 = 2/5-2/7 tách những cái kia tương tự góp vào rồi tính

Ta có: \(A=3\dfrac{1}{117}\cdot\dfrac{1}{119}-\dfrac{4}{117}\cdot5\dfrac{118}{119}-\dfrac{5}{117\cdot119}+\dfrac{8}{39}\)
\(=\dfrac{352}{117}\cdot\dfrac{1}{119}-\dfrac{4}{117}\cdot\dfrac{713}{119}-\dfrac{5}{117\cdot119}+\dfrac{8}{39}\)
\(=\dfrac{352-2852-5}{117\cdot119}+\dfrac{8}{39}\)
\(=\dfrac{-835}{4641}+\dfrac{8}{39}\)
\(=\dfrac{3}{119}\)

=(54⋅9+59⋅14+514⋅19+...+544⋅49)⋅1−(3+5+7+...+49)89=(54⋅9+59⋅14+514⋅19+...+544⋅49)⋅1−(3+5+7+...+49)89=15⋅(14−19+19−114+114−119+...+144−149)⋅(1−(52⋅24)289)=15⋅(14−19+19−114+114−119+...+144−149)⋅(1−(52⋅24)289)=15⋅(14−149)⋅1−62489=15⋅(14−149)⋅1−62489=15⋅45196⋅−62389=15⋅45196⋅−62389=−928
\(\dfrac{1}{4\cdot9}+\dfrac{1}{9\cdot14}+\dfrac{1}{14\cdot19}+...+\dfrac{1}{44\cdot49}\)
\(=\dfrac{1}{5}\left(\dfrac{9-4}{4\cdot9}+\dfrac{14-9}{9\cdot14}+\dfrac{19-14}{14\cdot19}+...+\dfrac{49-44}{44\cdot49}\right)\)
\(=\dfrac{1}{5}\cdot\left(\dfrac{1}{4}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{14}+\dfrac{1}{14}-\dfrac{1}{19}+....+\dfrac{1}{44}-\dfrac{1}{49}\right)\)
\(=\dfrac{1}{5}\cdot\left(\dfrac{1}{4}-\dfrac{1}{49}\right)\)
\(=\dfrac{1}{5}\cdot\dfrac{45}{196}\)
\(=\dfrac{9}{196}\)

\(B=\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}\)
\(B=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+\dfrac{1}{6\cdot7}\)
\(B=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}\)
\(B=1-\dfrac{1}{7}\)
\(B=\dfrac{6}{7}\)

a) \(1-\dfrac{1}{2}=\dfrac{1}{2}\)
\(\dfrac{1}{2}-\dfrac{1}{3}=\dfrac{3-2}{6}=\dfrac{1}{6}\)
\(\dfrac{1}{3}-\dfrac{1}{4}=\dfrac{4-3}{12}=\dfrac{1}{12}\)
\(\dfrac{1}{4}-\dfrac{1}{5}=\dfrac{5-4}{20}=\dfrac{1}{20}\)
\(\dfrac{1}{5}-\dfrac{1}{6}=\dfrac{6-5}{30}=\dfrac{1}{30}\)
b) \(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}\)
\(=\left(1-\dfrac{1}{2}\right)+\left(\dfrac{1}{2}-\dfrac{1}{3}\right)+\left(\dfrac{1}{3}-\dfrac{1}{4}\right)+\left(\dfrac{1}{4}-\dfrac{1}{5}\right)+\left(\dfrac{1}{5}+\dfrac{1}{6}\right)\)
\(=1+\left(-\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(-\dfrac{1}{3}+\dfrac{1}{3}\right)+\left(-\dfrac{1}{4}+\dfrac{1}{4}\right)+\left(-\dfrac{1}{5}+\dfrac{1}{5}\right)+-\dfrac{1}{6}\)\(=1+-\dfrac{1}{6}\)
\(=\dfrac{5}{6}\)
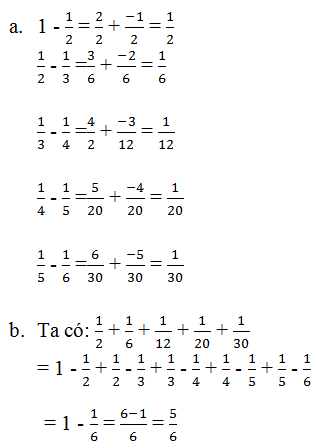
\(\dfrac{1}{5}+\dfrac{1}{20}+\dfrac{1}{44}+\dfrac{1}{77}+\dfrac{1}{119}+\dfrac{1}{170}+\dfrac{1}{230}+\dfrac{1}{299}\)
=\(\dfrac{2}{10}+\dfrac{2}{40}+\dfrac{2}{88}+\dfrac{2}{154}+\dfrac{2}{238}+\dfrac{2}{340}+\dfrac{2}{460}+\dfrac{2}{598}\)
=\(\dfrac{1}{3}.2\left(\dfrac{3}{2.5}+\dfrac{3}{5.8}+\dfrac{3}{8.11}+\dfrac{3}{11.14}+\dfrac{3}{14.17}+\dfrac{3}{17.20}+\dfrac{3}{20.23}+\dfrac{3}{23.26}\right)\)
=\(\dfrac{2}{3}\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{14}+\dfrac{1}{14}-\dfrac{1}{17}+\dfrac{1}{17}-\dfrac{1}{20}+\dfrac{1}{20}-\dfrac{1}{23}+\dfrac{1}{23}-\dfrac{1}{26}\right)\)
=\(\dfrac{2}{3}\left(\dfrac{1}{2}-\dfrac{1}{26}\right)\)
=\(\dfrac{2}{3}.\dfrac{6}{13}\)
=\(\dfrac{4}{13}\)