Chứng minh rằng\(\dfrac{1}{4^2} + \dfrac{1}{6^2} + \dfrac{1}{8^2} + ....... + \dfrac{1}{2n^2}< \dfrac{1}{4}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 4 2023
\(S=\dfrac{1}{2^2}\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}\right)\)
=>\(S< =\dfrac{1}{4}\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n-1}-\dfrac{1}{n}\right)\)
=>\(S< =\dfrac{1}{4}\cdot\left(1-\dfrac{1}{n}\right)=\dfrac{1}{4}\cdot\dfrac{n-1}{n}< =\dfrac{1}{4}\)
21 tháng 8 2018
Ta thấy: k2 > (k - 1)(k + 1)
Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{4^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}\)
\(< \dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{99.101}\)
\(=\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\right).\dfrac{1}{2}\)
\(=\left(1-\dfrac{1}{101}\right).\dfrac{1}{2}\)
\(=\dfrac{100}{101}.\dfrac{1}{2}< 1.\dfrac{1}{2}=\dfrac{1}{2}\)
11 tháng 3 2021
vì: \(\dfrac{1}{4^2}< \dfrac{1}{4}\)
\(\dfrac{1}{6^2}< \dfrac{1}{4}\)
........
\(\dfrac{1}{2020^2}< \dfrac{1}{4}\)
=> \(\dfrac{1}{4^2}+\dfrac{1}{6^2}+.......+\dfrac{1}{2020^2}< \dfrac{1}{4}\)
22 tháng 2 2022
a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)
b: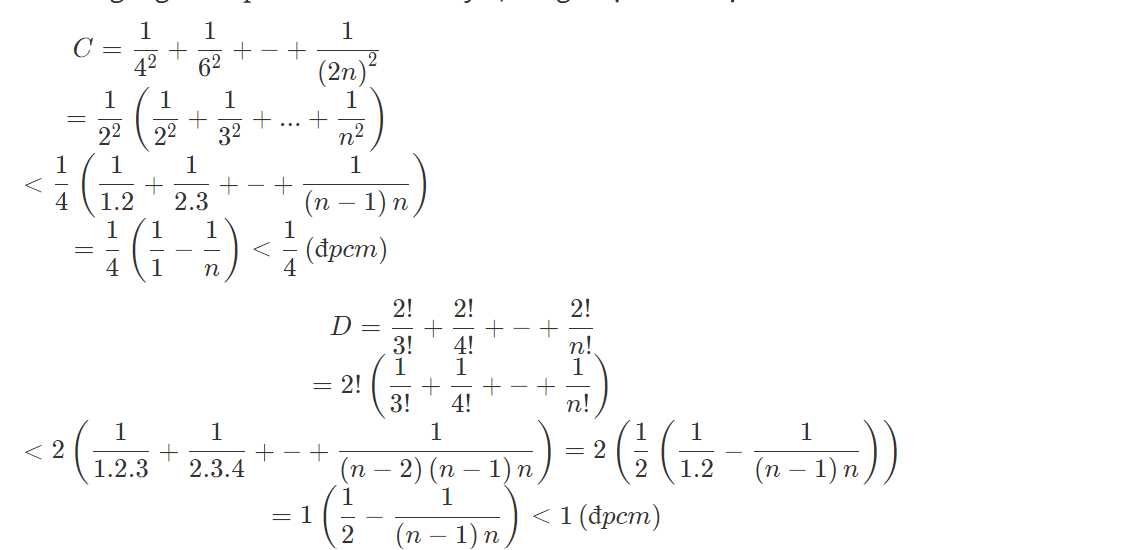 
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 3 2023
A = \(\dfrac{1}{2^2}\) + \(\dfrac{1}{4^2}\) + \(\dfrac{1}{6^2}\) + .....+ \(\dfrac{1}{1002^2}\)
A = \(\dfrac{1}{2^2.1^2}\) + \(\dfrac{1}{2^2.2^2}\) + \(\dfrac{1}{2^2.3^2}\)+......+\(\dfrac{1}{2^2.501^2}\)
A = \(\dfrac{1}{2^2}\) \(\times\)( \(1\) + \(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\)+.......+ \(\dfrac{1}{501^2}\))
ta có : \(\dfrac{1}{2^2}\) < \(\dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}\) < \(\dfrac{1}{2.3}\)
................
\(\dfrac{1}{501^2}\) < \(\dfrac{1}{500.501}\)
Cộng vế với vế ta được
\(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\) +.....+ \(\dfrac{1}{501^2}\) < \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+.......+\dfrac{1}{500.501}\)
\(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\) +.....+ \(\dfrac{1}{501^2}\) < \(\dfrac{1}{1}\) - \(\dfrac{1}{2}\) + \(\dfrac{1}{2}-\dfrac{1}{3}\)+.....+ \(\dfrac{1}{500}-\dfrac{1}{501}\)
\(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\)+......+ \(\dfrac{1}{501^2}\) < 1 - \(\dfrac{1}{501}\) < 1
=>A = \(\dfrac{1}{4}\) \(\times\) ( 1 + \(\dfrac{1}{2^2}\)+ \(\dfrac{1}{3^2}\)+.....+\(\dfrac{1}{501^2}\)) < \(\dfrac{1}{4}\) \(\times\)(1 + 1)
A < \(\dfrac{1}{4}\) \(\times\) 2
A < \(\dfrac{1}{2}\)
TG
11 tháng 4 2022
1/4^2 + 1/5^2 +... + 1/100^2 < 1/3.4 + 1/4.5 +...+ 1/99.100
A=1/3 - 1/4 + 1/4 - 1/5 +...+ 1/99 - 1/100
=1/3 - 1/100 < 1/3
NP
2
6 tháng 9 2021
\(\dfrac{1}{5^2}< \dfrac{1}{4.5}\)
\(\dfrac{1}{6^2}< \dfrac{1}{5.6}\)
......
\(\dfrac{1}{100^2}< \dfrac{1}{99.100}\)
\(\Rightarrow\dfrac{1}{5^2}+\dfrac{1}{6^2}+\dfrac{1}{7^2}+...+\dfrac{1}{100^2}< \dfrac{1}{4.5}+\dfrac{1}{5.6}+...+\dfrac{1}{99.100}=\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{99}-\dfrac{1}{100}=\dfrac{1}{4}-\dfrac{1}{100}< \dfrac{1}{4}\)
6 tháng 9 2021
Ta có: \(\dfrac{1}{5^2}+\dfrac{1}{6^2}+\dfrac{1}{7^2}+...+\dfrac{1}{100^2}< \dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{99.100}\)
\(=\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=\dfrac{1}{4}-\dfrac{1}{100}< \dfrac{1}{4}\)
Ta có:
\(\frac{1}{4^2}+\frac{1}{6^2}+\frac{1}{8^2}+...+\frac{1}{2n^2}\)
\(=\frac{1}{2}\left(\frac{2}{2.4}+\frac{2}{4.6}+\frac{2}{6.8}+...+\frac{2}{\left(2n-2\right).2n}\right)\)
\(=\frac{1}{2}\left(\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+\frac{1}{6}-\frac{1}{12}+...+\frac{1}{2n-2}-\frac{1}{2n}\right)\)
\(=\frac{1}{2}\left(\frac{1}{2}-\frac{1}{2n}\right)\)
\(=\frac{1}{4}-\frac{1}{2n.2}\)
Vì \(\frac{1}{4}-\frac{1}{2n.2}< \frac{1}{4}\)
\(\Rightarrow\frac{1}{4^2}+\frac{1}{6^2}+\frac{1}{8^2}+...+\frac{1}{2n^2}< \frac{1}{4}\)
Vậy \(\frac{1}{4^2}+\frac{1}{6^2}+\frac{1}{8^2}+...+\frac{1}{2n^2}< \frac{1}{4}\) (Đpcm)