Cho các số 0<a1<a2<a3<....<a15. chứng minh rằng (a1+a2+a3+...+a15)/(a5+a10+a15)<5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 5 2018
Chọn C.
Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải:
11 tháng 9 2021
\(15,\\ b,B=\left\{102;111;120;201;210;300\right\}\\ 16,\\ a,975310\\ b,907531\\ 17,\\ a,không.thay.đổi\\ b,gấp.10\\ c,gấp.10.và.+3\)
CM
28 tháng 11 2019
a, x – 9 = 13 => x = 13 + 9 => x = 22
Vậy M = {22} và M có 1 phần tử
b, x + 6 = 34
x = 34 – 6
x = 28
Vậy H = {28} và H có 1 phần tử.
c, x.0 = 0 luôn đúng với mọi x ∈ N
Vậy O = N và O có vô số phần tử
d, a) x.0 = 3 không thỏa mãn vì trong tập hợp các số tự nhiên, số nào nhân với 0 cũng bằng 0
Vậy A = { ∅ } và A có 0 phần tử
e, (x – 2)(x – 5) = 0
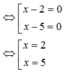
Vậy N = {2;5} và N có 2 phần tử
f, a) x : 0 = 0 không có số tự nhiên nào thỏa mãn vì không thể chia cho 0
Vậy G = { ∅ } và G có 0 phần tử
30 tháng 10 2017
Ta có :
2 các chọn chữ số hàng trăm
2 cách chọn chữ số hàng chục
1 cách chọn chữ số hàng đơn vị
Vậy lập được :
2 . 2 . 1 = 4 số
Các số đó là : ab0 ; a0b ; ba0 ; b0a
Tổng các số đó là :
ab0 + a0b + ba0 + b0a = a. 100 + b.10 + a.100 + b + b.100 + a.10 + b.100 + a
= a. ( 100 + 100 + 10 + 1 ) + b . ( 100 + 100 + 10 + 1 )
= a . 211 + b . 211
= 211 . ( a + b )
Vậy tổng trên chia hết cho 211
DD
Đoàn Đức Hà
Giáo viên
8 tháng 5 2021
Số \(2000020\)có chữ số \(2\)xuất hiện ở vị trí thứ \(7\)và vị trí thứ \(2\)nên nó xuất hiện ở vị trí thứ:
\(2\times2\times...\times2\)(\(6\)chữ số \(2\)) \(+2=64+2=66\).
TV
5
