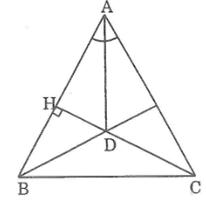
cho tam giác ABC. Đường cao BD, CE cắt nhau tại H.Biết ac=bh.Chứng minh rằng tam giác ABC có góc B Bằng 45 độ hoặc 135 độ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(\widehat{EBH}+\widehat{BHE}=\widehat{EBH}+\widehat{BAD}\left(=90^0\right)\)
Vì \(\widehat{EBH}\) chung => \(\widehat{BHE}=\widehat{BAD}.\)
Xét 2 \(\Delta\) vuông \(AEC\) và \(HEB\) có:
\(\widehat{AEC}=\widehat{HEB}=\left(=90^0\right)\)
AC = HB (gt)
\(\widehat{CAE}=\widehat{BHE}\left(=\widehat{DHC}\right)\)
=> \(\Delta AEC=\Delta HEB\) (cạnh huyền - góc nhọn).
=> EC = EB (2 cạnh tương ứng).
=> \(\Delta CEB\) cân tại E
mà \(\widehat{CEB}=90^0\)
=> \(\Delta CEB\) vuông cân tại E.
=> \(\widehat{EBC}\) \(\left(\widehat{B}\right)=45^0\left(đpcm\right)\)
Đây là trường hợp \(\widehat{B}\) nhọn, còn trường hợp \(\widehat{B}\) tù thì bạn làm tương tự sẽ tìm ra \(\widehat{B}=135^0\) nhé.
Chúc bạn học tốt!