Một ô tô chuyển động trên nửa đoạn đường đầu với vận tốc 15m/s. Phần đường còn lại, xe chuyển động với vận tốc 45 km/h trong nửa thời gian đầu và 15 km/h trong nửa thời gian sau. Tính vận tốc trung bình của ô tô trên cả quãng đường đã đi.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đổi \(15m/s=54km/h\)
Thời gian ô tô đi nửa đoạn đầu:
\(t_1=\frac{S_1}{v_1}=\frac{\frac{S}{2}}{54}=\frac{S}{108}\left(h\right)\)
Mặt khác,ta có:
\(S_2+S_3=\frac{S}{2}\)
\(\Leftrightarrow v_2\cdot t_2+v_3\cdot t_3=\frac{S}{2}\)
\(\Leftrightarrow v_2\cdot\frac{t'}{2}+v_3\cdot\frac{t'}{2}=\frac{S}{2}\)
\(\Leftrightarrow45t'+15t'=S\)
\(\Rightarrow t'=\frac{S}{60}\)
Ta có:
\(v_{tb}=\frac{S_1+S_2+S_3}{t_1+t_2+t_3}=\frac{S}{\frac{S}{108}+\frac{S}{60}}=\frac{270}{7}km/h\)
Đúng không ta ??

Giải:
Ta có vận tốc trung bình v = s 1 + s 2 + s 3 t 1 + t 2 + t 3
Giai đoạn một: S 1 = S 2 mà t 1 = S 1 v 1 = S 2 v 1 = 2 120 ( h )
Giai đoạn 2: S 2 = v 2 . t 2 = 40. t 2
Giai đoạn 3: S 3 = v 3 . t 3 = 20. t 3 mà t 2 = t 3 ⇒ s 3 = 20 t 2
Theo bài ra S 2 + S 3 = S 2 ⇒ 40 t 2 + 20 t 2 = S 2 ⇒ t 2 = t 3 = S 120 ( h )
⇒ v = S S 120 + S 120 + S 120 = 40 k m / h

Gọi x là nửa thời gian đi hết nửa qdg \(ab\Rightarrow\frac{1}{2}x\) là tg đi hết nữa quãng duường còn lại
=> nửa quãng dg đầu là 60x
\(\frac{1}{2}\) quãng dường còn lại là \(\frac{1}{2}x.40\)
\(\frac{1}{2}\) quãng dg cuối là \(\frac{1}{2}x.20\)
Ta có vận tốc :
\(vtb=\left[60x+40x+20x\right]:\left[\frac{1}{2}c+\frac{1}{2}x+x\right]=80x:2x=40\)km/h
Chuyển động của ô tô chia thành ba giai đoạn :
Giai đoạn 1: \(s_1=\frac{s}{2};v_1=60\frac{km}{h}\Rightarrow t_1=\frac{s}{120}\)
Giai đoạn 2 : \(s_2=40t_2\)
Giai đoạn 3 : \(s_3=20t_3;t_3=t_2\Rightarrow s_3=20t_2\)
Ta có : \(s_2+s_3=\frac{s}{2}\Rightarrow60t_2=\frac{s}{2}\Rightarrow t_2=\frac{s}{120}\left(h\right)\)
Thời gian đi cả đoạn đường :
\(t=t_1+2t_2=\frac{3s}{120}\)
Tốc độ tb " \(v_{tb}=\frac{s}{t}=\frac{49km}{h}\)

ta có:
vận tốc trung bình của người đó là:
\(v_{tb}=\frac{S_1+S_2+S_3}{t_1+t_2+t_3}=\frac{S}{t_1+t'}\left(1\right)\)
ta lại có:
\(t_1=\frac{S_1}{v_1}=\frac{S}{2v_1}=\frac{S}{120}\left(2\right)\)
mặt khác ta có:
\(S_2+S_3=\frac{S}{2}\)
\(\Leftrightarrow v_2t_2+v_3t_3=\frac{S}{2}\)
\(\Leftrightarrow\frac{v_2t'}{2}+\frac{v_1t'}{2}=\frac{S}{2}\)
\(\Leftrightarrow45t'+15t'=S\)
\(\Rightarrow t'=\frac{S}{60}\left(3\right)\)
thế (2) và (3) vào (1) ta có:
\(v_{tb}=\frac{S}{\frac{S}{120}+\frac{S}{60}}=\frac{S}{S\left(\frac{1}{120}+\frac{1}{60}\right)}=\frac{1}{\frac{1}{120}+\frac{1}{60}}=40\)
vậy vận tốc trung bình của người đó là 40km/h
một người đi từ A đến B gồm ba chặng chặng thứ nhất dài 20km mất 1 giờ 10 puhts. chặng thứ 2 dài 30km mất 1 giờ 20 phút. chặng thứ ba dài 40km mất 2 giờ. a) tìm vận tốc đi mỗi chặng đường.b) tính quãng đường AB
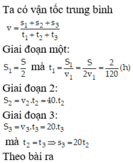
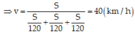

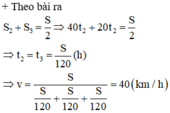
Đổi: 45km/h=12,5m/s, 15km/h=25/6m/s
Gọi độ dài quãng đường là S(m)
Thời gian đi hết quãng đường đầu là: t1=S/30(s)
Gọi thời gian ô tô đi hết nửa quãng đường sau là t (s)
=> Vận tốc trung bình của ô tô ở nửa quãng đường sau là: v2=(12,5.t/2+25/6.t/2)t=25/3(m/s)
=> t=t2=3.S/50(s)
Ta có: t1/t2=5/9 => t1=5/9.t2
=> Vận tốc trung bình của ô tô trên cả quãng đường là: vtb=15.t1+25/3.t2/t1+t2=(25/3.t2+25/3.t2)/(14/9).t2=75/7(m/s)
Đổi 15m/s = 54km/h
Gọi v1 là vận tôc trên nửa đoạn đường đầu
v2 là vận tốc cd trong nửa thời gian đầu của phần đường còn lại
v3 là vận tốc cd trong phần thời gian còn lai của quãng đường
Vận tốc trung bình của ô tô trong phần đường còn lại
Vtb1 = (v2 +v3)/2 =(45 + 15 )/2 =30 km/h
vận tốc tb của ô tô trên cả quãng đường
Vtb = AB/ t1 + t2 <=> AB/(AB/2V1)+(AB/2Vtb1)
tối giản AB ta đc
2V1.Vtb1/ V1+ Vtb1 (thay số vào thì ra kết quả)