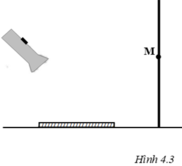
Một gương phẳng nhỏ MN đặt song song với 1 bức tường mặt gương quay vào tường trước gương có 1 nguồn sáng điểm A
a. Hãy vẽ 1 tia sáng xuất phát từ điểm A phản xạ trên gương rồi đi đến điểm B trên tường .
b. Hãy vẽ phần của tường được ánh sáng phản xạ của gương chiếu sáng .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

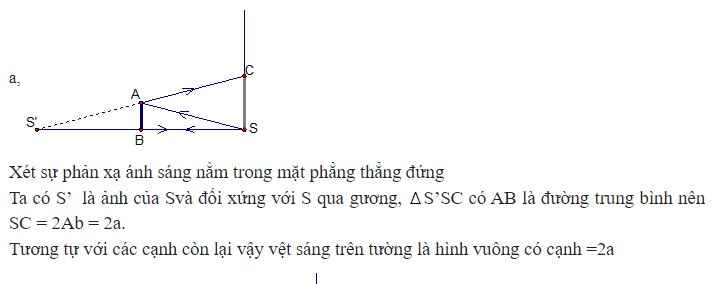
a, 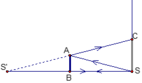
Xét sự phản xạ ánh sáng nằm trong mặt phẳng thẳng đứng
Ta có S’ là ảnh của Svà đối xứng với S qua gương, ∆ S’SC có AB là đường trung bình nên SC = 2Ab = 2a.
Tương tự với các cạnh còn lại vậy vệt sáng trên tường là hình vuông có cạnh =2a
b, 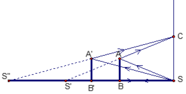
Khi nguồn sáng S ở sát chân tườngvà di chuyển gương theo phương vuông góc với tường(đến gần hoặc ra xa tường)thì kích thước của vệt sáng không thay đổi. Luôn là hinhg vuông cạnh là 2a. Vì SC luôn bằng 2AB = 2a
Trong khoảng thời gian t gương di chuyển với vận tốc v và đi được quãng đường BB’ = vt.
Cũng trong thời gian đó ảnh S’ của S dịch chuyển với vận tốc v’ và đi được quãng đường S’S” = v’t
Theo tính chất ảnh và vật đối xứng nhau qua gương ta có:
SB’ = B’S” <=>SB + BB’ = B’S’+S’S” (1)
SB = BS’ <=> SB = BB’ + B’S’ (2)
Thay (2) và (1) ta có: BB’ + B’S’+ BB’ = B’S’+S’S” <=> 2BB’ = S’S”
Hay v’t = 2vt <=> v’ =2v

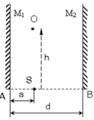
a) Chọn S1 đối xứng S qua gương M1 ; Chọn O1 đối xứng O qua gương M2 , nối S1O1 cắt gương M1 tại I , gương M2 tại J. Nối SIJO ta được tia cần vẽ
b) DS1AI ~ D S1BJ
Þ A I B J = S 1 A S 1 B = a a + d
Þ AI = a a + d .BJ (1)
Xét DS1AI ~ D S1HO1
Þ A I H O 1 = S 1 A S 1 H = a 2 d
Þ AI = a 2 d . h thay vào (1) ta được BJ = ( a + d ) . h 2 d


a) vẽ hình như trên.
b) chứng minh hai tia JR // SI
Ta có do hai pháp tuyển N1 và N2 vuông góc nên ta có \(i'+i_1 = 90^0\)
mà \(i=i'; i_1 = i_1' => i+i'+i_1+i_1' = 90+90 = 180^0\)
=> JR//SI (tổng hai góc trong cùng phía bằng 180 độ)

Cách vẽ:
Gọi: S' là ảnh của S qua gương 1.
\(\Rightarrow\) Tia tới qua gương 1 tạo ra tia phản xạ đi qua S'.
Gọi: S'' là ảnh của S qua gương 2.
\(\Rightarrow\) Tia tới khi qua gương 2 cho tia phản tạo ta tia phản xạ đi qua S
\(\Rightarrow\) Tia tới sẽ đi qua S''.
Giả sử S', S'' cắt G tại A và G' tại B.
\(\Rightarrow\) SABS là đường truyền tia sáng cần vẽ.
Chứng minh:
Ta có: \(\left\{{}\begin{matrix}\widehat{SAG}=\widehat{OAB}\\\widehat{OBA}=\widehat{SBG'}\end{matrix}\right.\)
\(\widehat{ASB}+\widehat{SAB}+\widehat{SBA}=90^0\)
\(\widehat{SAB}+2\widehat{OAB}=180^0\) \(\Rightarrow\widehat{SAB}=180^0-2\widehat{0AB}\)
\(\widehat{SBA}+2\widehat{OAB}=180^0\Rightarrow\widehat{SBA}=180^0-2\widehat{OAB}\)
\(\Rightarrow\widehat{ASB}+180^0-2\widehat{0AB}+180^0-2\widehat{OBA}=180^0\)
\(\Leftrightarrow\widehat{ASB}+2\left(180^0-\widehat{0AB}-\widehat{0BA}\right)=180^0\)
\(\Leftrightarrow\widehat{ASB}+2\alpha=180^0\)
\(\Rightarrow\widehat{ASB}=180^0-2\alpha\)
Vậy \(\widehat{ASB}\) không phụ thuộc vào góc tới mà phụ thuộc vào góc hợp bởi 2 gương (đpcm).

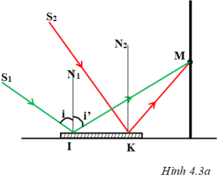
Muốn có được 2 tia tới cho hai tia phản xạ cùng tới điểm M trên tường thì ta phải thay đổi vị trị của đèn sao cho mỗi vị trí đó ứng với một tia tới SI cho tia phản xạ IM.
* Thay đổi vị trí đèn để có tia SI, vị trí này được xác định như sau:
+ Lấy điểm tới I bất kì trên gương, nối IM ta được tia phản xạ IM.
+ Vẽ pháp tuyến IN1 tại điểm tới, rồi vẽ góc tới 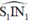 bằng góc phản xạ
bằng góc phản xạ 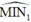 nghĩa là:
nghĩa là: 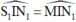 . Ta xác định được tia tới S1I cũng chính là vị trí đặt đèn pin.
. Ta xác định được tia tới S1I cũng chính là vị trí đặt đèn pin.
* Tương tự như vậy ta vẽ được tia tới S2K ứng với vị trí thứ hai của đèn pin.