2. Cho tam giác ABC có góc A = 90o (AB<AC ), phân giác BE. Lấy H thuộc BC, sao cho BH = BA.
a) CM: EH thuộc BC, so sánh AE và EC
b) CM: BE là đường trung trực của AH
c) Đường thẳng EH và AB cắt nhau ở K
CM: EK = EC
d) C: AH song song KC
E) Gọi M là trung điểm của KC, CM: B,E,M THẲNG HÀNG

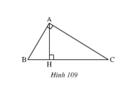
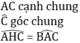
a: Xét ΔBAE và ΔBHE có
BA=BH
\(\widehat{ABE}=\widehat{HBE}\)
BE chung
DO đó: ΔBAE=ΔBHE
Suy ra: \(\widehat{BAE}=\widehat{BHE}=90^0\)
Ta có: EA=EH
mà EH<EC
nên EA<EC
b: Ta có: BA=BH
EA=EH
DO đó: BE là đường trung trực của AH
c: Xét ΔAEK vuông tại A và ΔHEC vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)
Do đó: ΔAEK=ΔHEC
SUy ra: EK=EC