Cho AB và CD là hai đoạn thẳng song song và bằng nhau, A'B' và C'D' là các hình chiếu của chúng trên cùng một đường thẳng. Chứng minh rằng A'B' = C'D'
GIÚP MK VS NHA. CẢM ƠN MỌI NGƯỜI NHIỀU Ạ
@soyeon_Tiểubàng giải
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho AB và CD là hai đoạn thẳng song song và bằng nhau, A'B' và C'D' là các hình chiếu của chúng trên cùng một đường thẳng. Chứng minh rằng A'B' = C'D'
GIÚP MK VS NHA. CẢM ƠN MỌI NGƯỜI NHIỀU Ạ
@soyeon_Tiểubàng giải
1 câu trả lời
Toán lớp 7 Ôn tập toán 7

Từ A hạ đường vuông góc với BB' tại H
Từ C hạ đường vuông góc với DD' tại K
Gọi I là giao điểm của CD và BB'
Dễ thấy BB' // DD' do cùng _|_ A'D'
=> BID = IDK (so le trong)
Lại có: ABI = BID (so le trong)
=> IDK = ABI
Xét t/g ABH vuông tại H và t/g CDK vuông tại K có:
AB = CD (gt)
ABH = CDK (cmt)
Do đó, t/g ABH = t/g CDK ( cạnh huyền - góc nhọn)
=> AH = CK (2 cạnh tương ứng) (1)
Có: AH // A'B' ( cùng _|_ BB')
AA' // B'H ( cùng _|_ A'D')
=> AH = A'B' ( tính chất đoạn chắn) (2)
Tương tự ta cũng có: CK = C'D' (3)
Từ (1); (2) và (3) => A'B' = C'D' (đpcm)
Bài này có trong câu hỏi tương tự bạn nên tìm nhé :)))
Mình dán lên đây cho bạn xem cho tiện

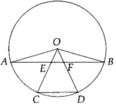
a, Chứng minh được ∆OEA = ∆OFB => AE = FB
b, Chứng minh được O E F ^ = O C D ^ => AB//CD
Bài này có 1 số trường hợp hình, tương ứng với mỗi trường hợp sẽ là 1 cách giải, các cách giải khá giống nhau. Ở đây t lm trường hợp đơn giản nhất: A'B' và C'D' có điểm trong chung tức là C' nằm giữa A' và B'; B' nằm giữa C' và D'
Từ A hạ đường vuông góc với BB' tại H
Từ C hạ đường vuông góc với DD' tại K
Gọi I là giao điểm của CD và BB'
Dễ thấy BB' // DD' do cùng _|_ A'D'
=> BID = IDK (so le trong)
Lại có: ABI = BID (so le trong)
=> IDK = ABI
Xét t/g ABH vuông tại H và t/g CDK vuông tại K có:
AB = CD (gt)
ABH = CDK (cmt)
Do đó, t/g ABH = t/g CDK ( cạnh huyền - góc nhọn)
=> AH = CK (2 cạnh tương ứng) (1)
Có: AH // A'B' ( cùng _|_ BB')
AA' // B'H ( cùng _|_ A'D')
=> AH = A'B' ( tính chất đoạn chắn) (2)
Tương tự ta cũng có: CK = C'D' (3)
Từ (1); (2) và (3) => A'B' = C'D' (đpcm)