Tìm đa thức f(x) biết rằng f(x) chia cho x+3 thì dư 1, chia cho x-4 thì dư 8, chia cho (x+3)(x-4) thì được thương là 3x và còn dư
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
7 tháng 2 2018
Em tham khảo bài tương tự tại đây nhé.
Câu hỏi của Bạch Quốc Huy - Toán lớp 8 - Học toán với OnlineMath
1 tháng 9 2018
1)
Đặt \(f\left(x\right)=ax^4+bx^3+cx^2+dx+e.\)( a khác 0 )
Ta có:
\(f\left(1\right)=a+b+c+d+e=0\) (1)
\(f\left(2\right)=16a+8b+4c+2d+e=0\) (2)
\(f\left(3\right)=81a+27b+9c+3d+e=0\) (3)
\(f\left(4\right)=256a+64b+16c+4d+e=6\) (4)
\(f\left(5\right)=625a+125b+25c+5d+e=72\) (5)
\(A=f\left(2\right)-f\left(1\right)=15a+7b+3c+d=0\)
\(B=f\left(3\right)-f\left(2\right)=65a+19b+5c+d=0\)
\(C=f\left(4\right)-f\left(3\right)=175a+37b+7c+d=6\)
\(D=f\left(5\right)-f\left(4\right)=369a+61b+9c+d=72-6=66\)
\(E=B-A=50a+12b+2c=0\)
\(F=C-B=110a+18b+2c=6\)
\(G=D-C=194a+24b+2c=66-6=60\)
Tiếp tục lấy H=F-E; K=G-F; M=H-K
Ta tìm được a
Thay vào tìm được b,c,d,e
2 tháng 9 2018
1. gọi đa thức cần tìm là f(x) =a.x^4+b.x^3+c.x^2+dx+e
có f(1)=f(2)=f(3) = 0 nên x=1,2,3 la nghiệm của f(x) = 0 vậy f(x) có thể viết dưới dạng f(x) = (x-1)(x-2)(x-3)(mx+n)
thay f(4)=6 và f(5)=72 tìm được m =2 và n= -7
Vậy đa thức f(x) =(x-1)(x-2)(x-3)(2x-7) => e = (-1).(-2).(-3).(-7) = 42
Với x=2010 thì (a 2010^4+b.2010^3+c.2010^2+d.2010 ) luôn chia hết 10 vậy số dư f(2010) chia 10 = số dư d/10 = 2 (42 chia 10 dư 2).
2. Thiếu dữ liệu
3. đa thức f(x) chia đa thức (x-3) có số dư là 2 =>bậc f(x) = bậc (x-3)=1 và f(x) = m.(x-3) +2=mx+2-3m (1)
...........................................(x+4)...................9..........................................f(x) = n(x+4) + 9=nx+4n+9 (2)
để (1)(2) cùng xảy ra thì m=n và (2-3m)=(4n+9) => m = n = -1 khi đó đa thức f(x) = -x +5
Không hiếu dữ liệu cuối f(x) chia 1 đa thức bậc 2 lại có thương là 1 đa thức bậc 2? => vô lý
12 tháng 2 2020
Từ đề bài ta có \(f\left(x\right)=A\left(x\right).\left(x-3\right)+2\Rightarrow f\left(3\right)=2\)
\(f\left(x\right)=B\left(x\right).\left(x+4\right)+9\Rightarrow f\left(-4\right)=9\)
\(f\left(x\right)=\left(x^2+3\right).\left(x^2+x-12\right)+\left(x^2+3\right).\left(ax+b\right)=\left(x^2+3\right).\left(x-3\right).\left(x+4\right)+\left(x^2+3\right).\left(ax+b\right)\left(1\right)\)Từ (1).Ta có \(f\left(3\right)=\left(3^2+3\right)\left(3a+b\right)=36a+12b\Rightarrow36a+12b=2\)
\(f\left(-4\right)=\left(\left(-4\right)^2+3\right)\left(-4a+b\right)=-76a+19b\Rightarrow-76a+19b=9\)
Giải hệ phương trình ẩn a,b ta tìm được a,b.Từ đó thế vào (1).Ta tìm được f(x)
CH
Cô Hoàng Huyền
Admin
VIP
7 tháng 2 2018
Câu hỏi của Bạch Quốc Huy - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo bài tương tự tại đây nhé.
29 tháng 3 2020
f(x)= (x-3). Q(x)+2 moi X
f(x)=(x+4).H(x)+9 moi X
=>f(3)= 2
f( -4)= 9
f(x)= (x^2+x-12).(x^2+3)+ ax +b
=(x-3)(x+4). (x^2+3) +ax+b
=>f(3)= 3a+b=2
f(-4)=b -4a=9
=>a= -1; b=5
=> f(x)=(x^2+x-12)(x^2+3)-x+5
= x^4+x^3-9x^2+2x-31
# mui #
LT
21 tháng 1 2015
Vì f(x) chia cho x2-5x+6 được thương là 1-x2 và còn dư nên f(x) có bậc 4 và đa thức dư bậc cao nhất là 1.
Gọi f(x)=(x-2)(x-3)(1-x2)+ax+b
Ta có f(2)=2 vaf(3)=7 thay vào tìm đc a và b suy ra đa thức f(x) cần tìm.
Giải giùm nha!!
CH
Cô Hoàng Huyền
Admin
VIP
7 tháng 2 2018
Câu hỏi của Bạch Quốc Huy - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo bài tương tự tại đây nhé.
15 tháng 4 2021
Vì f(x) chia x-3 dư 7
\(\Rightarrow f\left(x\right)=\left(x-3\right)q\left(x\right)+7\)
\(\Rightarrow f\left(3\right)=7\)
Vì f(x) chia x-2 dư 5
\(\Rightarrow f\left(x\right)=\left(x-2\right)q\left(x\right)+5\)
\(\Rightarrow f\left(2\right)=5\)
Ta có f(x) khi chia (x-2)(x-3) thì được thương là 3x và còn dư
\(\Rightarrow f\left(x\right)=\left(x-2\right)\left(x-3\right)3x+ax+b\)
\(\Rightarrow\hept{\begin{cases}f\left(2\right)=2a+b=5\\f\left(3\right)=3a+b=7\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a=2\\b=1\end{cases}}\)
Vậy \(f\left(x\right)=\left(x-2\right)\left(x-3\right)3x+2x+1\)
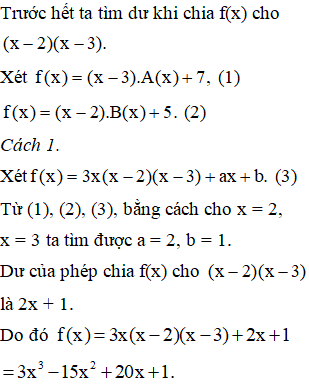
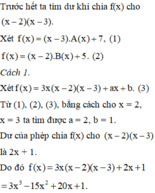
F(x) = ( x + 3 )( x - 4 ).3x + ax + b
F(-3) = 1 => -3a + b = 1 => b = 1 + 3a
F(4) = 8 => 4a + b = 8 thay b = 1 + 3a
=> 7a + 1 = 8 => a = 1 => b = 1 + 3 = 4
=> f(x) = ( x + 3 )( x - 4 ).3x + x + 4
đến đây chỉ việc nhân ra thôi