mọi người giúp mình giải hai câu này được không ạ 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1A
Sau ''where'' là S và căn cứ vào nghĩa của câu nha em
2A
Trước ''whom'' là chủ ngữ chỉ người và ''girl'' là đối tượng được nghĩ tới
Câu 2 này giải thích vậy không biết em có hiểu không :)))?

a: \(=\dfrac{x+2}{x+2}=1\)
b: \(=\dfrac{2x+6}{x+3}=2\)

Câu 1:
const fi='dulieu.dat';
fo='thaythe.out';
var f1,f2:text;
a:array[1..100]of string;
n,d,i,vt:integer;
begin
assign(f1,fi); reset(f1);
assign(f2,fo); rewrite(f2);
n:=0;
while not eof(f1) do
begin
n:=n+1;
readln(f1,a[n]);
end;
for i:=1 to n do
begin
d:=length(a[i]);
vt:=pos('anh',a[i]);
while vt<>0 do
begin
delete(a[i],vt,3);
insert('em',a[i],vt);
vt:=pos('anh',a[i]);
end;
end;
for i:=1 to n do
writeln(f2,a[i]);
close(f1);
close(f2);
end.
Câu 2:
uses crt;
const fi='mang.inp';
fo='sapxep.out';
var f1,f2:text;
a:array[1..100]of integer;
i,n,tam,j:integer;
begin
clrscr;
assign(f1,fi); rewrite(f1);
assign(f2,fo); rewrite(f2);
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
for i:=1 to n do
write(f1,a[i]:4);
for i:=1 to n-1 do
for j:=i+1 to n do
if a[i]>a[j] then
begin
tam:=a[i];
a[i]:=a[j];
a[j]:=tam;
end;
for i:=1 to n do
write(f2,a[i]:4);
close(f1);
close(f2);
end.

\(x^2+2x+1=x^2+2\cdot1x+1^2=\left(x+1\right)^2\)
\(4x^2+12x+9=\left(2x\right)^2+2\cdot3\cdot2x+3^2=\left(2x+3\right)^2\)
\(\dfrac{4}{9}a^2-\dfrac{4}{3}a+1=\left(\dfrac{2}{3}a\right)^2-2\cdot\dfrac{2}{3}\cdot1a+1^2=\left(\dfrac{2}{3}a-1\right)^2\)
\(a^2+5a+\dfrac{25}{4}=a^2+2\cdot2,5a+2,5^2=\left(2,5+a\right)^2\)

\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên

8.
\(sin\left(2x-\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{3}=-\dfrac{\pi}{6}+k2\pi\\2x-\dfrac{\pi}{3}=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{12}+k\pi\\x=\dfrac{3\pi}{4}+k\pi\end{matrix}\right.\)
\(\Rightarrow x=\left\{-\dfrac{11\pi}{12};\dfrac{\pi}{12};-\dfrac{\pi}{4};\dfrac{3\pi}{4}\right\}\)
Pt có 4 nghiệm trong khoảng đã cho
9.
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{12}+k2\pi\\x=-\dfrac{7\pi}{12}+k2\pi\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{23\pi}{12};\dfrac{17\pi}{12}\right\}\)
Pt có 2 nghiệm trên khoảng đã cho


Câu 4:
a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(Cạnh huyền-góc nhọn)

TXĐ: `D=RR\\{π/2+kπ ; -π/4 +kπ}`
Mà `-π/2+k2π` và `π/2+k2π \in π/2 +kπ`
`=>` Không nằm trong TXĐ.






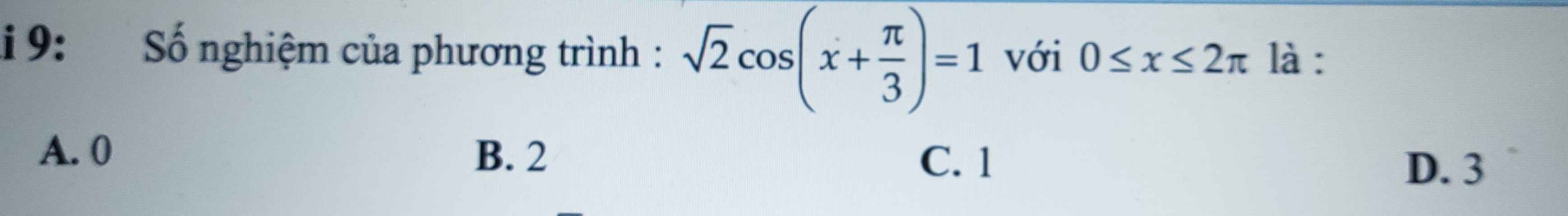

Bài 4:
a) Ta có: AM+MB=AB
AN+NC=AC
mà MB=NC
và AB=AC
nên AM=AN
Xét ΔABC có
\(\dfrac{AM}{MB}=\dfrac{AN}{NC}\)
nên MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
b) Ta có: ΔABC cân tại A
nên \(\widehat{B}=\widehat{C}=\dfrac{180^0-\widehat{A}}{2}=\dfrac{180^0-40^0}{2}=70^0\)
\(\Leftrightarrow\widehat{BMN}=\widehat{CNM}=180^0-70^0=110^0\)
Bài 3:
Ta có: ABCD là hình thang cân
nên AD=BC
mà AD=AB
nên BC=AB
Xét ΔBAC có BA=BC(cmt)
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)(hai góc ở đáy)
mà \(\widehat{BAC}=\widehat{ACD}\)(hai góc so le trong, AB//CD
nên \(\widehat{BCA}=\widehat{DCA}\)
hay CA là tia phân giác của \(\widehat{BCD}\)