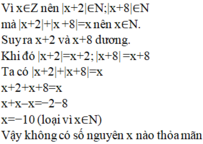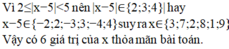có bao nhiêu số nguyên x thỏa mãn 2<gttd của x +3/2<=19/4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Ta có: 9,5<x<17,7
mà x là số nguyên
nên \(x\in\left\{10;11;12;...;17\right\}\)
Số số hạng thỏa mãn là 17-10+1=8(số)
b: Ta có: -1,23<x<2,5
mà x là số nguyên
nên \(x\in\left\{-1;0;1;2\right\}\)
=>Có 4 số thỏa mãn

a)Vì x,y ko âm =>x,y>0
=>ko tồn tại
b)Có vô số nghiệm x,y
Vd:1 và 0
-2 và 3
-3 và 4
.....

Đáp án B.
Điều kiện: x − 40 > 0 60 − x > 0 ⇔ 40 < x < 60 . Khi đó ta có:
log x − 40 + log 60 − x < 2 ⇔ log x − 40 60 − x < 2 ⇔ x − 40 60 − x < 10 2
x 2 − 100 x + 2500 > 0 ⇔ x − 50 2 > 0 ⇔ x ≠ 50
(do x − 50 2 ≥ 0 với mọi x).
Kết hợp với điều kiện ta có x ∈ 40 ; 60 \ 50 .
Suy ra có 60 − 40 − 1 − 1 = 18 số nguyên dương thỏa mãn điều kiện đã cho.
Lưu ý: Lỗi sai thường gặp: x − 50 2 > 0 ⇔ x > 50 ; x − 50 2 > 0
thỏa mãn với mọi x ∈ ℝ .

=>x(y+1)+y+1=3
=>(y+1)(x+1)=3
=>\(\left(x+1;y+1\right)\in\left\{\left(1;3\right);\left(3;1\right);\left(-1;-3\right);\left(-3;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(0;2\right);\left(2;0\right);\left(-2;-4\right);\left(-4;-2\right)\right\}\)
=>Có 4 cặp

\(x^2+2017x\le2018x+2019\)
\(\Rightarrow x^2-x-2019\le0\)
Ta có: \(VT=x^2-x-2019=x^2-2.x.\frac{1}{2}+\frac{1}{4}-\frac{1}{4}-2019\)
\(=\left(x-\frac{1}{2}\right)^2-\frac{8077}{4}\)
\(=\left(x-\frac{1}{2}-\sqrt{\frac{8077}{4}}\right)\left(x-\frac{1}{2}+\sqrt{\frac{8077}{4}}\right)\le0\)
\(\Rightarrow\frac{1}{2}-\sqrt{\frac{8077}{4}}\le x\le\frac{1}{2}+\sqrt{\frac{8077}{4}}\)
Do x nguyên nên \(-44\le x\le45\)
Auto làm nốt