Question

[chu thị ánh nguyệt]

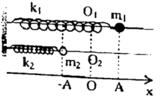
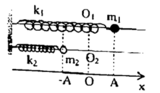
hai con lắc lò xo giống nhau treo cùng vào 2 điểm trên cùng giá đỡ nằm ngang trọn õ thẳng đứng xuống dưới. pt dao động của 2 con lắc lần lượt là x₁=3 cos(10\(\sqrt{3}\)t ) (cm) ; x₂=4 cos(10\(\sqrt{3}\)t +\(\pi\)/2 ) (cm), biết lò xo có k=50N/m

a, tỉ số Wđ_max của 2 dao động bằng bao nhiêu?

b, hợp lực do2 con lắc tác dụng lên giá đỡ có độ lớn cực đại gần giá trị nào nhất?

Answer 1

[Nguyễn Hoàng Việt]

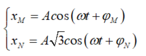
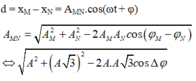
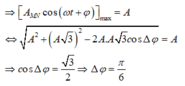
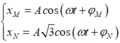
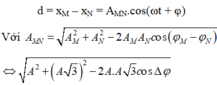
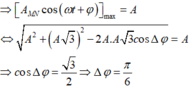
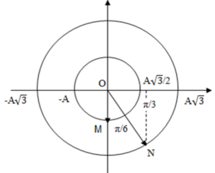
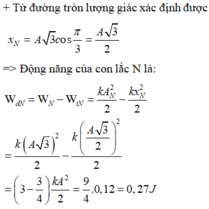
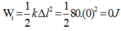
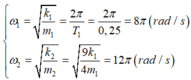
a) \(W_{đmax}=W\) \(\Rightarrow\frac{W_{đ1max}}{W_{đ2max}}=\frac{W_1}{W_2}=\frac{kA_1^2}{kA_2^2}=\frac{3^2}{4^2}=\frac{9}{16}\)

b) Hợp lực tác dụng lên giá đỡ bằng tổng lực đàn hồi tác dụng lên 2 lò xo

\(F=k\left(\Delta l_0+x_1\right)+k\left(\Delta l_0+x_1\right)=k\left(2\Delta l_0+x_1+x_2\right)\)

\(F max \Leftrightarrow x_1+x_2 max\)

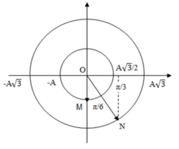
Mà hai lò xo dao động vuông pha, cùng tần số với nhau nên \(max\left(x_1+x_2\right)=\sqrt{x_1^2+x_2^2}=0,05\left(m\right)\)

Vậy \(F_{max}=k\left(2\Delta l_0+0,05\right)=50\left(2\cdot\frac{g}{\omega^2}+0,05\right)=\frac{35}{6}\left(N\right)\)