cho hs y= \(\frac{2X-1}{X-1}\) .viết phương trình tiếp tuyến của đồ thị hàm số...biết khoảng cách từ I(1;2) đến tiếp tuyến bằng \(\sqrt{2}\)
giúp e với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Ta có y’ = x2 + 2x và y” = 2x + 2
Theo giả thiết xo là nghiệm của phương trình y”(xo) = 0
⇔ 2x + 2 = 0 ⇔ xo = -1
Và y’(-1) = -1
Phương trình tiếp tuyến tại điểm 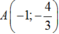 là: y = -1.(x + 1) - 7/3
là: y = -1.(x + 1) - 7/3
Hay  .
.

Giao điểm với trục tung B(0 ;-1). Ta có
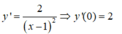
Hệ số góc của tiếp tuyến của đồ thị hàm số 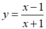 tại giao điểm của đồ thị hàm số với trục tung bằng k = 2.
tại giao điểm của đồ thị hàm số với trục tung bằng k = 2.
Chọn B

Ta có y ' = x 2 + 2 x và y" = 2x + 2.
- Theo giả thiết x 0 là nghiệm của phương trình y " ( x 0 ) = 0 .
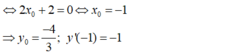
- Phương trình tiếp tuyến tại điểm 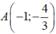 là:
là:
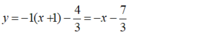
Chọn A.

- Ta có :
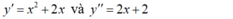
- Theo giả thiết x 0 là nghiệm của phương trình:
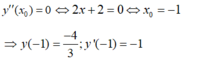
- Phương trình tiếp tuyến tại điểm 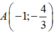 là:
là:
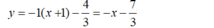
Chọn A.
Lời giải:
Giả sử tiếp điểm có hoành độ $x_0$. Phương tình tiếp tuyến tại tiếp điểm là:
\(y=f'(x_0)(x-x_0)+f(x_0)=\frac{-x}{(x_0-1)^2}+\frac{2x_0^2-2x_0+1}{(x_0-1)^2}\) (\(\Delta\))
Khoảng cách từ \(\Delta\) đến \(I(1,2)\) là :
\(d=\frac{\left | \frac{-1}{(x_0-1)^2}-2+\frac{2x_0^2-2x_0+1}{(x_0-1)^2} \right |}{\sqrt{\frac{1}{(x_0-1)^4}+1}}=\sqrt{2}\Rightarrow x_0\in\left \{0;2 \right \}\)
Do đó có 2 PTTT là:\(\left\{\begin{matrix}y=-x+1\\ y=-x+5\end{matrix}\right.\)